(4) A Predator-Prey Model

Model Description

Suppose there is a population of rabbits (prey) and a population of foxes (predators) that inhabit the same area. The sizes of these two populations can be modeled as a system of ordinary differential equations (ODEs). In particular, if $x$ and $y$ represent the numbers (in thousands) of rabbits and foxes, respectively, the rates of change of these numbers can be estimated as
$\begin{align} \frac{\textrm{d}x}{\textrm{d}t} &= \alpha x - \beta x y, \\ \frac{\textrm{d}y}{\textrm{d}t} &= \gamma x y - \delta y, \\ \end{align}$ where $\alpha$ (day $^{-1}$ ) is a parameter that determines the birth rate of rabbits, $\beta$ (day $^{-1}$ per 1000 foxes) is a parameter that determines the death rate of rabbits, $\gamma$ (day $^{-1}$ per 1000 rabbits) is a parameter that determines the birth rate of foxes, and $\delta$ (day $^{-1}$ ) is a parameter that determines the death rate of foxes. In order to solve an initial value problem for the predator-prey model, one needs to provide the values of $\alpha$ , $\beta$ , $\gamma$ , and $\delta$ , as well as initial values for $x$ and $y$ .

MCSim Model Specification

We used the GNU MCSim model specification language to implement the predator-prey model. The complete MCSim model specification file for this model, pred_prey.model, can be found in the extdata subdirectory of the MCSimMod package.

In the model specification file, we used the text symbols x and y to represent the state variables $x$ and $y$ and the text symbols alpha, beta, gamma, and delta to represent the parameters $\alpha$ , $\beta$ , $\gamma$ , and $\delta$ , respectively.

Building the Model

First, we load the MCSimMod package as follows.

library(MCSimMod)
#> Loading required package: tools

Using the following commands, we create a model object (i.e., an instance of the Model class) using the model specification file pred_prey.model that is included in the MCSimMod package.

# Get the full name of the package directory that contains the example MCSim
# model specification file.
mod_path <- file.path(system.file(package = "MCSimMod"), "extdata")

# Create a model object using the example MCSim model specification file
# "pred_prey.model" included in the MCSimMod package.
pp_mod_name <- file.path(mod_path, "pred_prey")
pp_mod <- createModel(pp_mod_name)

Once the model object is created, we can “load” the model (so that it’s ready for use in a given R session) as follows.

# Load the model.
pp_mod$loadModel()
#> C compilation complete. Full details are available in the file /tmp/Rtmphx5q4m/compiler_output.txt.
#> Hash created and saved in the file /tmp/Rtmphx5q4m/pred_prey_model.md5.

Predicting the Numbers of Rabbits and Foxes

Suppose we want to predict the numbers of rabbits and foxes over a period of 50 days assuming that $\alpha = 0.67$ , $\beta = 1.33$ , $\gamma = 1.00$ , $\delta = 1.00$ , and the initial numbers of rabbits and foxes are 1000 and 750, respectively. These are the default values of the model parameters and initial conditions that are provided in the model specification file, and we can verify this with the following commands.

pp_mod$parms
#> alpha  beta gamma delta 
#>  0.67  1.33  1.00  1.00
pp_mod$Y0
#>    x    y 
#> 1.00 0.75

We can perform a simulation that provides results for the desired output times (i.e., $t = 0.0, 0.1, 0.2, \ldots, 50.0$ ) using the following commands.

# Define output times for simulation.
times <- seq(from = 0, to = 50, by = 0.1)

# Run simulation.
out <- pp_mod$runModel(times)

Examining the Results

The final command shown above, out <- pp_mod$runModel(times), performs a model simulation and stores the simulation results in a “matrix” data structure called out. There is one row for each output time, and one column for each state variable. The first five rows of this data structure are shown below. Note that the independent variable, which is $t$ in the case of the predator-prey model, is always labeled “time” in the output data structure.

time	x	y
0.0	1.0000000	0.7500000
0.1	0.9678346	0.7487880
0.2	0.9369984	0.7452243
0.3	0.9077112	0.7394507
0.4	0.8801364	0.7316377

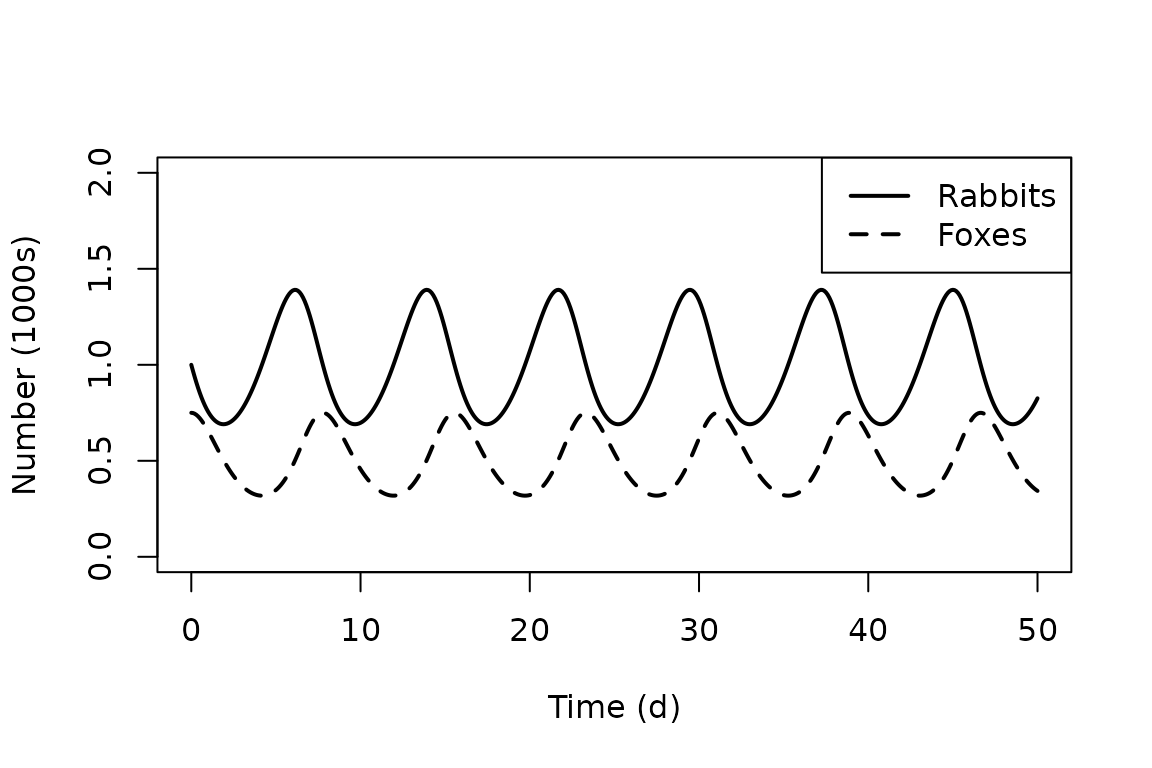
We can create visual representations of the simulation results. For example, we can plot the numbers of rabbits and foxes vs. time using the following commands.

# Plot simulation results (numbers vs. time).
plot(out[, "time"], out[, "x"],
  type = "l", lty = 1, lwd = 2,
  xlab = "Time (d)", ylab = "Number (1000s)", ylim = c(0, 2)
)
lines(out[, "time"], out[, "y"], lty = 2, lwd = 2)
legend("topright", c("Rabbits", "Foxes"),
  lty = c(1, 2),
  lwd = 2
)

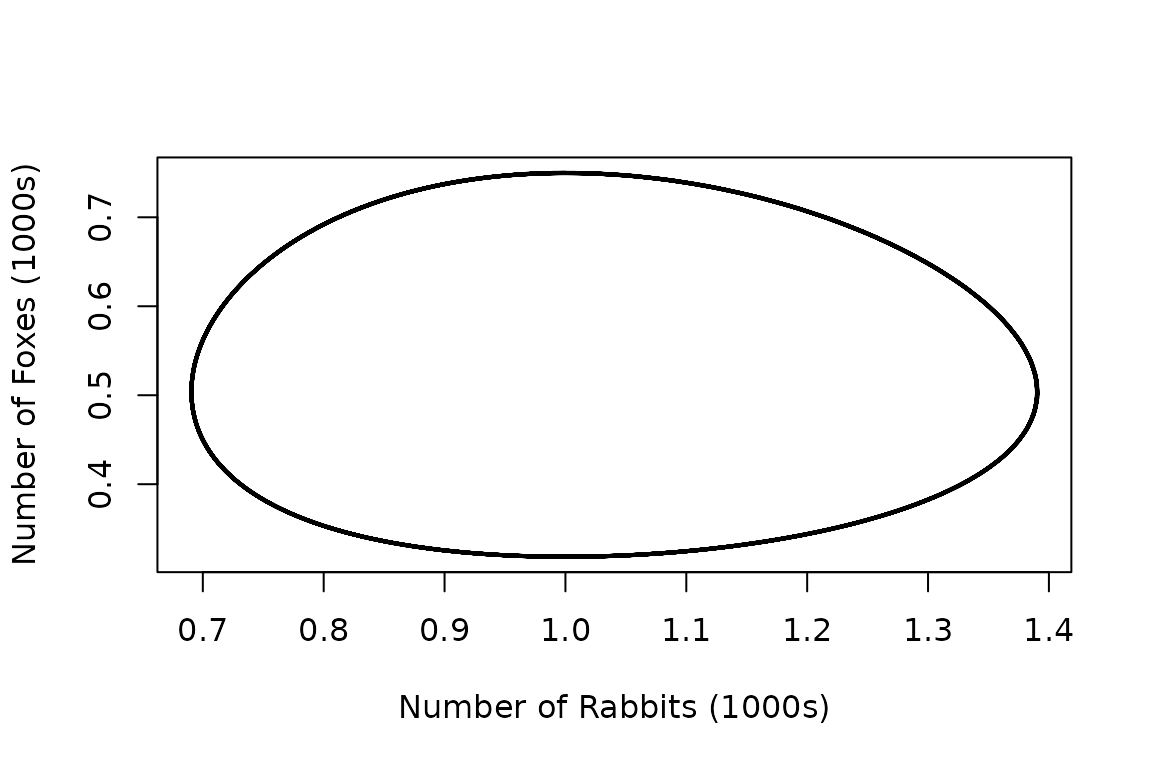
Alternatively, we can plot the results in phase-space as follows.

# Plot simulation results (number of foxes vs. number of rabbits).
plot(out[, "x"], out[, "y"],
  type = "l", lty = 1, lwd = 2,
  xlab = "Number of Rabbits (1000s)", ylab = "Number of Foxes (1000s)"
)

Removing Output Files

We can remove output files that were created when building the model (i.e., files with names ending in “.c”, “.o”, “_inits.R”, and “.dll” or “.so”) by calling the cleanup() method.

# Remove output files that were created when building the model.
pp_mod$cleanup()