An Introduction to Spatial Stream Network Modeling in R Using SSN2

Michael Dumelle, Erin Peterson, Jay M. Ver Hoef, Alan Pearse, and Dan Isaak

Background

Data from streams frequently exhibit unique patterns of spatial autocorrelation resulting from the branching network structure, longitudinal (i.e., upstream/downstream) connectivity, directional water flow, and differences in flow volume throughout the network (Erin E. Peterson et al. 2013). In addition, stream networks are embedded within a spatial environment, which can also influence observations on the stream network. Traditional spatial statistical models, which are based solely on Euclidean distance, often fail to adequately describe these unique and complex spatial dependencies.

Spatial stream network models are based on a moving-average construction (J. M. Ver Hoef and Peterson 2010) and are specifically designed to describe two unique spatial relationships found in streams data. A pair of sites is considered flow-connected when water flows from an upstream site to a downstream site. Sites are flow-unconnected when they reside on the same stream network (i.e., share a common junction downstream) but do not share flow.

Spatial stream network models typically rely on two families of covariance functions to represent these relationships: the tail-up and tail-down models. In a tail-up model, the moving-average function points in the upstream direction. Covariance is a function of stream distance and a weighting structure used to proportionally allocate, or split, the function at upstream junctions to account for differences in flow volume or other influential variables (Erin E. Peterson and Ver Hoef 2010). As a result, non-zero covariances are restricted to flow-connected sites in a tail-up model. In a tail-down model, the moving average function points in the downstream direction. In contrast to the tail-up model, tail-down models allow for both flow-connected and flow-unconnected autocorrelation, autocorrelation will always be equal or stronger for flow-unconnected sites than flow-connected sites separated by equal stream distances (J. M. Ver Hoef and Peterson 2010). In the tail-down model, covariance is a function of stream distance and weights are not required. However, it is also possible and often preferable to build spatial stream network models based on a mixture of four components: a tail-up component, a tail-down component, a Euclidean component, and a nugget component. The Euclidean component is useful because it captures covariance in influential processes that are independent of the stream network at intermediate and broad scales (e.g., air temperature, soil type, or geology). The nugget component captures covariance in processes that are highly localized, thus being independent across sites. For more details regarding the construction of spatial stream network models and their covariance components, see Cressie et al. (2006), J. M. Ver Hoef, Peterson, and Theobald (2006), J. M. Ver Hoef and Peterson (2010), Erin E. Peterson and Ver Hoef (2010), and Isaak et al. (2014).

The SSN2 R package is used to fit and summarize spatial stream network models and make predictions at unobserved locations (Kriging). SSN2 is an updated version of the SSN R package (J. Ver Hoef et al. 2014). Why did we create SSN2 to replace the SSN R package? There are two main reasons:

1. The SSN R package depends on the rgdal (Bivand, Keitt, and Rowlingson 2021), rgeos (Bivand and Rundel 2020), and maptools (Bivand and Lewin-Koh 2021) R packages, which were retired in October, 2023. Their functionality has been replaced and modernized by the sf package (Pebesma 2018). SSN2 depends on sf instead of rgdal, rgeos, and maptools, reflecting this broader change regarding handling spatial data in R.

   • See Nowosad (2023) for more information regarding the retirement of rgdal, rgeos, and maptools, available at this link.

2. There are features added to SSN2 that would have been difficult to implement in the SSN R package without a massive restructuring of its foundation, so a new package was created. For example, the SSN objects in SSN2 are S3 objects but the SSN objects in the SSN R package were S4 objects. Additionally, many functions were rewritten and/or repurposed in SSN2 to use generic functions (e.g., block prediction in SSN2 is performed using predict() while in the SSN R package it was performed using BlockPredict()). Moreover, SSN2 leverages many of the tools in the spmodel R package for spatial statistical modeling (Dumelle, Higham, and Ver Hoef 2023).

This vignette provides an overview of basic features in SSN2. We load SSN2 by running

library(SSN2)

If you use SSN2 in a formal publication or report, please cite it. Citing SSN2 lets us devote more resources to it in the future. We view the SSN2 citation by running

citation(package = "SSN2")

#> To cite SSN2 in publications use:
#> 
#>   Dumelle M, Peterson EE, Ver Hoef JM, Pearse A, Isaak DJ (2024). SSN2:
#>   The next generation of spatial stream network modeling in R. Journal
#>   of Open Source Software, 9(99), 6389,
#>   https://doi.org/10.21105/joss.06389
#> 
#> A BibTeX entry for LaTeX users is
#> 
#>   @Article{,
#>     title = {{SSN2}: The next generation of spatial stream network modeling in {R}},
#>     author = {Michael Dumelle and Erin E. Peterson and Jay M. {Ver Hoef} and Alan Pearse and Daniel J. Isaak},
#>     journal = {Journal of Open Source Software},
#>     year = {2024},
#>     volume = {9},
#>     number = {99},
#>     pages = {6389},
#>     doi = {10.21105/joss.06389},
#>     url = {https://doi.org/10.21105/joss.06389},
#>     publisher = {The Open Journal},
#>   }

Input Data

The streams, observation, and prediction datasets must be pre-processed prior to fitting SSN models and making predictions at unobserved locations using SSN2. Previously, the STARS toolset for ArcGIS Desktop versions 9.3x - 10.8x (E. Peterson and Ver Hoef 2014) or the openSTARS R package (kattwinkel2020preparing?) were used to generate spatial information required for model fitting and prediction. However, both software packages have recently been retired and are replaced by the SSNbler R package (Erin E. Peterson et al. 2024), which is a new, R-based version of the STARS tools. SSNbler is currently available on GitHub (link here), will soon be available on CRAN, and contains several useful resources that guide users through these pre-processing steps. Pre-processing using either SSNbler, STARS, or openSTARS ends with the creatino of a .ssn folder, which is non-proprietary. Files residing in the .ssn folder are read into R using ssn_import() from SSN2 and palced into a list structure called an SSN object, which contains all the spatial, topological, and attribute information needed to leverage the modeling tools in SSN2. This includes:

1. edges: a geopackage of lines representing the linear geometry of the stream network(s).
2. sites: a geopackage of site locations where observed data were collected on the stream network.
3. prediction sites: one or more geopackages of locations where predictions will be made. Optional.
4. netIDx.dat for each stream network: a text file containing topological relationships for the line segments in edges, by network.

SSN Objects in SSN2

The data contained in the .ssn object are read into R and stored as an SSN object, which has a special list structure with four elements:

1. edges: An sf object that contains the edges with LINESTRING geometry (representing the linear geometry of the stream network/s). The endpoints of the edges are called nodes.
2. obs: An sf object that contains the observed data with POINT geometry.
3. preds A list of sf objects with POINT geometry, each containing a set of locations where predictions will be made.
4. path: A character string that represents the path to the relevant .ssn directory stored on your computer.

A netgeom (short for “network geometry”) column is also added to each of the sf objects stored within an SSN object. The netgeom column contains a character string describing the position of each line (edges) and point (obs and preds) feature in relation to one another. The format of the netgeom column differs depending on whether it is describing a feature with LINESTRING or POINT geometry. For edges, the format of netgeom is

"ENETWORK (netID rid upDist)",

and for sites

"SNETWORK (netID rid upDist ratio pid locID)",

The data used to define the netgeom column are found in the edges, observed sites, and prediction sites geopackages, which are created using the SSNbler (recommended), STARS, or openSTARS software. For edges, this includes a unique network identifier (netID) and reach (i.e., edge) identifier (rid), as well as the distance between the most downstream location on the stream network (i.e., stream outlet) to the upstream node of each edge segment, when movement is restricted to the stream network (upDist). The netgeom column for sites also contains the netID and rid for the edge on which the site resides. The point identifier (pid) is unique to each measurement, while the location identifier (locID) is unique to each spatial location. Note that a locID may have multiple pids associated with it if there are repeated measurements in the observed data or multiple predictions are made at the same location. The upDist value for each site represents the stream distance between the stream outlet and the site location. Finally, the ratio is used to describe the relative position of a site on its associated edge segment. It is the proportional distance from the most downstream node of the edge segment to the site location. For example, ratio at a site is close to zero when the site is close to the most downstream node of the edge segment, and ratio at a site is close to one when the site is far from the most downstream node of the edge segment. Together these key pieces of data are used to describe which network and edge each site resides on, as well as where exactly the site is on each line segment. It may at first seem redundant to combine and store multiple numeric columns as text in the netgeom column. However, these data dictate how the observed and prediction sites relate to one another in topological space, which impacts parameter estimates and predicted values generated from fitted models. Storing these data as text in the netgeom column significantly reduces the chance that these values are accidentally (and unknowingly) altered by a user.

The Middle Fork Data

In this vignette, we will use the Middle Fork 2004 stream temperature data in SSN2. The raw input data are stored in the lsndata/MiddleFork04.ssn directory installed alongside SSN2. We may store the file path to this example data:

path <- system.file("lsndata/MiddleFork04.ssn", package = "SSN2")

Several functions in SSN2 for reading and writing data (which we use shortly) directly manipulate the .ssn folder. If it is not desirable to directly manipulate the MiddleFork04.ssn data installed alongside SSN2, MiddleFork04.ssn may be copied it into a temporary directory and the relevant path to this alternative location can be stored:

copy_lsn_to_temp()
path <- file.path(tempdir(), "MiddleFork04.ssn")

After specifying path (using system.file() or copy_lsn_to_temp()), we import the stream reaches, observed sites, and prediction sites:

mf04p <- ssn_import(
  path = path,
  predpts = c("pred1km", "CapeHorn"),
  overwrite = TRUE
)

We summarise the mf04p data by running

summary(mf04p)

#> Object of class SSN
#> 
#> Object includes observations on 26 variables across 45 sites within the bounding box
#>       xmin       ymin       xmax       ymax 
#> -1531384.6   914394.3 -1498447.7   933487.5 
#> 
#> Object also includes 2 sets of prediction points with a total of 829 locations
#> 
#> Variable names are (found using ssn_names(object)):
#> $obs
#>  [1] "rid"        "pid"        "STREAMNAME" "COMID"      "AREAWTMAP" 
#>  [6] "SLOPE"      "ELEV_DEM"   "Source"     "Summer_mn"  "MaxOver20" 
#> [11] "C16"        "C20"        "C24"        "FlowCMS"    "AirMEANc"  
#> [16] "AirMWMTc"   "rcaAreaKm2" "h2oAreaKm2" "ratio"      "snapdist"  
#> [21] "upDist"     "afvArea"    "locID"      "netID"      "netgeom"   
#> [26] "geometry"  
#> 
#> $pred1km
#>  [1] "rid"        "pid"        "COMID"      "AREAWTMAP"  "SLOPE"     
#>  [6] "ELEV_DEM"   "FlowCMS"    "AirMEANc"   "AirMWMTc"   "rcaAreaKm2"
#> [11] "h2oAreaKm2" "ratio"      "snapdist"   "upDist"     "afvArea"   
#> [16] "locID"      "netID"      "netgeom"    "geom"      
#> 
#> $CapeHorn
#>  [1] "rid"        "pid"        "COMID"      "AREAWTMAP"  "SLOPE"     
#>  [6] "ELEV_DEM"   "FlowCMS"    "AirMEANc"   "AirMWMTc"   "rcaAreaKm2"
#> [11] "h2oAreaKm2" "ratio"      "snapdist"   "upDist"     "afvArea"   
#> [16] "locID"      "netID"      "netgeom"    "geom"

We see that mf04p contains 45 observation sites and a total of 829 prediction sites stored in two different prediction datasets. We will explore several of these variables throughout the rest of the vignette:

• AREAWTMAP: Precipitation (area-weighted in mm)
• ELEV_DEM: Elevation (based on a 30m DEM)
• Summer_mn: Summer mean stream temperature (Celsius)
• C16: Number of times daily stream temperature exceeded 16 Celsius (in the summer)

A more detailed description of all the variables in mf04p is available in the documentation and can be seen by running ?MiddleFork04.ssn or help(MiddleFork04.ssn, package = "SSN2"). SSN2 currently does not have a generic plotting function for SSN objects. Instead, we rely on the plotting functionality of ggplot2 (Wickham 2016) and sf (Pebesma 2018). This vignette focuses on the use of ggplot2, which we load by running

library(ggplot2)

ggplot2 is only installed alongside SSN2 when dependencies = TRUE in install.packages(), so check that it is installed before reproducing any visualizations in this vignette.

Prediction sites can be easily accessed in the SSN object using the list element number or names attribute. For example, we print the names of the prediction datasets to the console

names(mf04p$preds)

#> [1] "pred1km"  "CapeHorn"

We view the Middle Fork stream network, overlay the observed sites where data were collected using brown circles, and overlay the pred1km prediction locations using smaller, blue triangles by running

ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = mf04p$preds$pred1km, pch = 17, color = "blue") +
  geom_sf(data = mf04p$obs, color = "brown", size = 2) +
  theme_bw()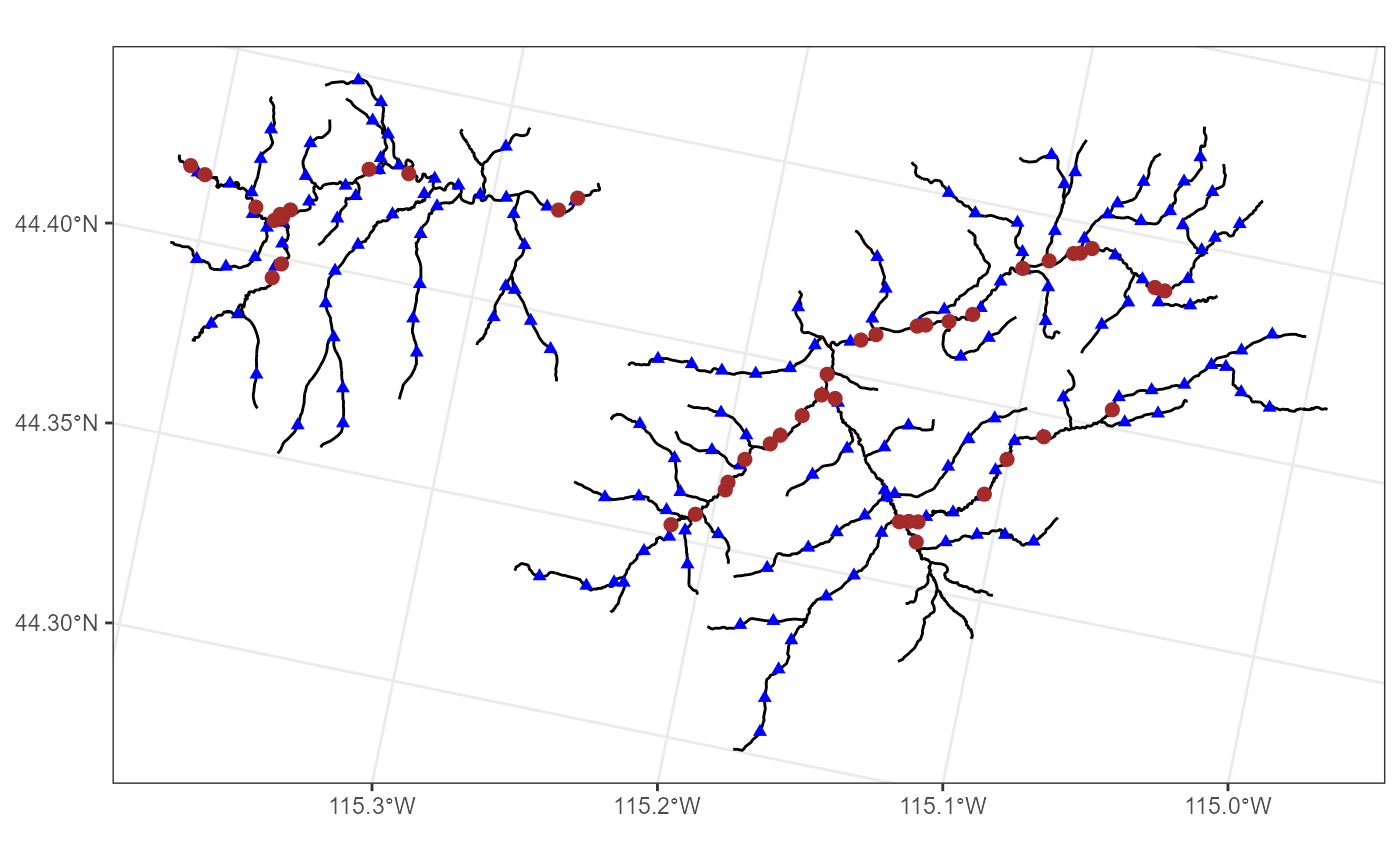

Later we will fit models to stream network data. Before doing this, however, we supplement the .ssn object with hydrologic distance matrices that preserve directionality, which are required for statistical modeling:

ssn_create_distmat(
  ssn.object = mf04p,
  predpts = c("pred1km", "CapeHorn"),
  among_predpts = TRUE,
  overwrite = TRUE
)

Stream distance matrices are saved as local files the .ssn directory associated with the SSN object, mf04p$path, in a folder called distance created by ssn_create_distmat(). The matrices are stored as .Rdata files in separate sub-folders for observed sites (obs) and each set of prediction sites. If the file path to the .ssn directory is incorrect, the ssn_update_path() can be used to update it before the distance matrices are generated.

Spatial Stream Network (SSN) Models

Linear SSN Models

We begin by fitting linear models to stream network data using the ssn_lm() function. Later we fit generalized linear models to stream network data using the ssn_glm() function. Typically, linear models are used when the response variable (i.e., dependent variable) is continuous and not highly skewed, and generalized linear models are often used when the response variable is binary, a count, or highly skewed.

Linear spatial stream network models for a quantitative response vector \(\mathbf{y}\) have spatially dependent random errors and are often parameterized as

\[\begin{equation*} \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\tau}_{tu} + \boldsymbol{\tau}_{td} + \boldsymbol{\tau}_{eu} + \boldsymbol{\epsilon}, \end{equation*}\]

where \(\mathbf{X}\) is a matrix of explanatory variables (usually including a column of 1’s for an intercept), \(\boldsymbol{\beta}\) is a vector of fixed effects that describe the average impact of \(\mathbf{X}\) on \(\mathbf{y}\), \(\boldsymbol{\tau}_{tu}\) is a vector of spatially dependent (autocorrelated) tail-up random errors, \(\boldsymbol{\tau}_{td}\) is a vector of spatially dependent (autocorrelated) tail-down random errors, \(\boldsymbol{\tau}_{eu}\) is a vector of spatially dependent (autocorrelated) Euclidean random errors, and \(\boldsymbol{\epsilon}\) is a vector of spatially independent (uncorrelated) random errors. The spatial dependence of each \(\boldsymbol{\tau}\) term is explicitly specified using a spatial covariance function that incorporates the variance of the respective \(\boldsymbol{\tau}\) term, often called a partial sill, and a range parameter that controls the behavior of the respective spatial covariance. The variance of \(\boldsymbol{\epsilon}\) is often called the nugget (or nugget effect). Sometimes several unconnected networks are modeled simultaneously. For two observations on separate networks, tail-up and tail-down random errors are uncorrelated but Euclidean random errors can be autocorrelated.

Suppose we are interested in studying summer mean temperature (Summer_mn) on the stream network. We can visualize the distribution of summer mean temperature (overlain onto the stream network) by running

ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = mf04p$obs, aes(color = Summer_mn), size = 2) +
  scale_color_viridis_c(limits = c(0, 17), option = "H") +
  theme_bw()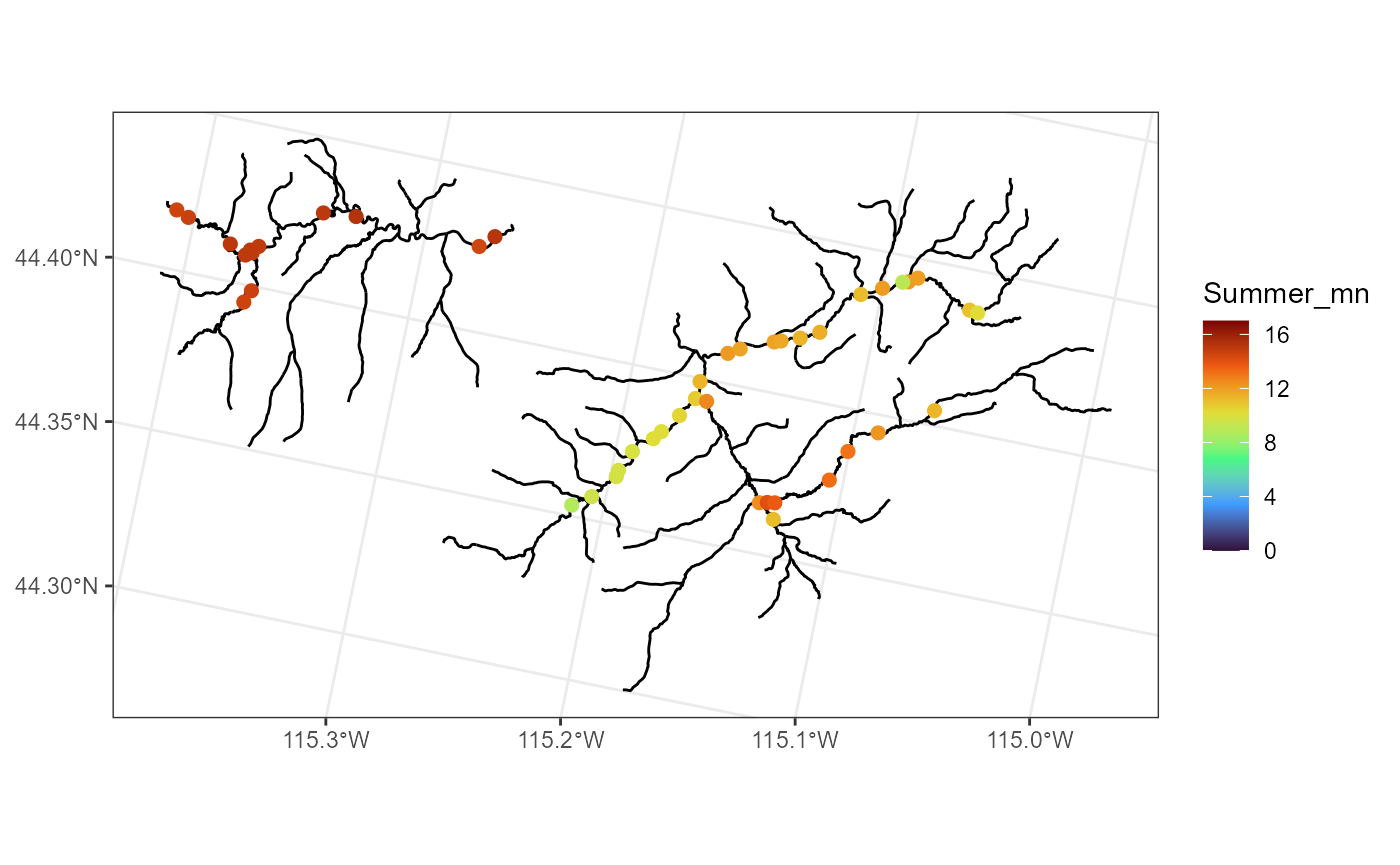

The ssn_lm() function is used to fit linear spatial stream network models and bears many similarities to base-R’s lm() function for non-spatial linear models. Below we provide a few commonly used arguments to ssn_lm():

• formula: a formula that describes the relationship between the response variable and explanatory variables.
  • formula uses the same syntax as the formula argument in lm().
• ssn.object: the .ssn object.
• tailup_type: the tail-up covariance, can be "linear", "spherical", "exponential", "mariah", "epa", or "none" (the default)
• taildown_type: the tail-down covariance, can be "linear", "spherical", "exponential", "mariah", "epa", or "none" (the default)
• euclid_type: the Euclidean covariance, can be "spherical", "exponential", "gaussian", "cosine", "cubic", "pentaspherical", "wave", "jbessel", "gravity", "rquad", "magnetic", or "none" (the default)
• nugget_type: "nugget" (the default) or "none".

It is important to note that the default for tailup_type, taildown_type, and euclid_type is "none", which means that they must be specified if their relevant covariances are desired. The default for nugget_type is "nugget", which specifies a nugget effect, useful because many ecological processes have localized variability that is important to capture. Full parameterizations of each covariance function are given in ssn_lm()’s documentation, which can be viewed by running help("ssn_lm", "SSN2"). There are different approaches to choosing between covariance functions. One approach is to fit several models and compare their fits using statistics like AIC or cross-validation error. Another approach is to visualize the Torgegram() and choose functions appropriately.

The Torgegram() in SSN2 is essentially a semivariogram that describes variability in streams data based on flow-connected, flow-unconnected, and Euclidean spatial relationships. Like other semivariograms, the Torgegram describes how the semivariance (i.e. halved average squared difference) between observations changes with hydrologic or Euclidean distances. If there is strong dependence between sites based on flow-connected or flow-unconnected relationships, the semivariance will increase with respective distance. If, however, there is not strong dependence, the semivariance will be relatively flat. The Torgegram() output can be combined with plot() to better understand which covariance components may be most suitable in the model. For example, when the semivariance for flow-connected sites increases with hydrologic distance but the semivariance for flow-unconnected sites is flat, then a tail-up component may be sufficient for the model (i.e., a tail-down component is not needed). However, the model would likely benefit from a tail-down component or a combination of tail-up and tail-down models if the semivariance for both flow-connected and flow-unconnected sites increases with distance. Alternatively, if the semivariance is flat, then the model is unlikely to benefit from tail-up or tail-down components. SSN2 also allows users to visualize changes in semivariance based on Euclidean distance, which may provide additional insights about whether a Euclidean component or a mixture of tail-up, tail-down and/or Euclidean models will improve the model. Please see Zimmerman and Ver Hoef (2017) for a more in-depth review of Toregegrams, along with strategies for interpreting and using them to inform model fitting. For a more formal comparison between models, use statistics like AIC or cross-validation error, which we discuss later.

Suppose that we want to model summer mean stream temperature as a function of elevation and precipitation. We can aid our understanding of what covariance components may be informative by visualizing a Torgegram:

tg <- Torgegram(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  type = c("flowcon", "flowuncon", "euclid")
)

The first argument to Torgegram() is formula. Residuals from a non-spatial linear model specified by formula are used by the Toregram to visualize remaining spatial dependence. The type argument specifies the Torgegram types and has a default value of c("flowcon", "flowuncon") for both flow-connected and flow-unconnected semivariances. Here we also desire to visualize Euclidean semivariance. We visualize all three components by running

plot(tg)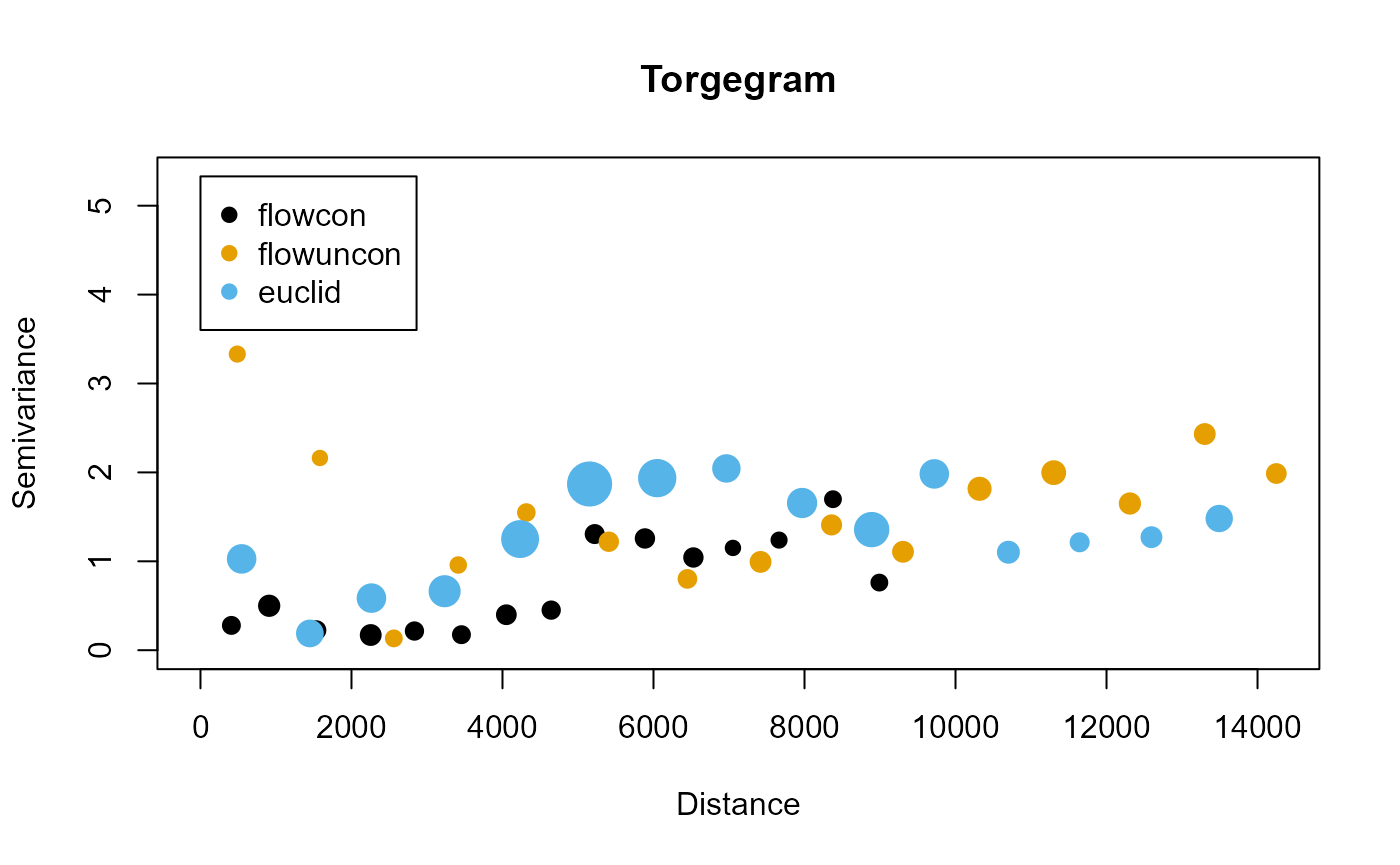

The flow-connected semivariances seem to generally increase with distance, which suggests that the model will benefit from at least a tail-up component. The takeaway for flow-unconnected and Euclidean semivariances is less clear – they seem to generally increase with distance but there are some short distances with high semivariances. We more empirically investigate the impact of each dependence structure next while we fit a model with all three components: tail-up, tail-down, and Euclidean.

We fit a spatial stream network model regressing summer mean stream temperature on elevation and watershed-averaged precipitation using an exponential tail-up covariance function with additive weights created using watershed area (afvArea), a spherical tail-down covariance function, a Gaussian Euclidean covariance function, and a nugget effect by running

ssn_mod <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea"
)

The estimation method is specified via the estmethod argument, which has a default value of "reml" for restricted maximum likelihood (REML). The other estimation method is "ml" for maximum likelihood (ML). REML is chosen as the default because it tends to yield more accurate covariance parameter estimates than ML, especially for small sample sizes. One nuance of REML, however, is that comparisons of likelihood-based statistics like AIC are only valid when the models have the same fixed effects structure (i.e., the same formula). To compare fixed effects and covariance structures simultaneously, use ML or a model comparison tool that is not likelihood-based, such as cross validation via loocv(), which we discuss later.

Model Summaries

We summarize the fitted model by running

summary(ssn_mod)

#> 
#> Call:
#> ssn_lm(formula = Summer_mn ~ ELEV_DEM + AREAWTMAP, ssn.object = mf04p, 
#>     tailup_type = "exponential", taildown_type = "spherical", 
#>     euclid_type = "gaussian", additive = "afvArea")
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -2.73430 -1.43161 -0.04368  0.83251  1.39377 
#> 
#> Coefficients (fixed):
#>              Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) 78.214857  12.189379   6.417 1.39e-10 ***
#> ELEV_DEM    -0.028758   0.005808  -4.952 7.35e-07 ***
#> AREAWTMAP   -0.008067   0.004125  -1.955   0.0505 .  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Pseudo R-squared: 0.4157
#> 
#> Coefficients (covariance):
#>               Effect     Parameter   Estimate
#>   tailup exponential  de (parsill)  1.348e+00
#>   tailup exponential         range  8.987e+05
#>   taildown spherical  de (parsill)  2.647e+00
#>   taildown spherical         range  1.960e+05
#>      euclid gaussian  de (parsill)  1.092e-04
#>      euclid gaussian         range  1.805e+05
#>               nugget        nugget  1.660e-02

Similar to summaries of lm() objects, summaries of ssn_lm() objects include the original function call, residuals, and a coefficients table of fixed effects. The (Intercept) represents the average summer mean stream temperature at sea level (an elevation of zero) and no precipitation, ELEV_DEM represents the decrease in average summer mean stream temperature with a one unit (meter) increase in elevation, and AREAWTMAP represents the decrease in average summer mean stream temperature with a one unit (mm) increase in precipitation. There is strong evidence that average summer mean stream temperature decreases with elevation (\(p\)-value \(< 0.001\)), while there is moderate evidence that average summer mean stream temperature decreases with precipitation (\(p\)-value \(\approx\) 0.05). A pseudo r-squared is also returned, which quantifies the proportion of variability explained by the fixed effects. The coefficients table of covariance parameters describes the model’s dependence. The larger the de parameter, the more variability in the process is attributed to the relevant effect. Here, most of the model’s random variability comes from the tail-up and tail-down portions of the model. The larger the range parameter, the more autocorrelated nearby observations are with respect to the relevant effect.

We directly compare the sources of variability in the model using the varcomp function:

varcomp(ssn_mod)

#> # A tibble: 5 × 2
#>   varcomp            proportion
#>   <chr>                   <dbl>
#> 1 Covariates (PR-sq)  0.416    
#> 2 tailup_de           0.196    
#> 3 taildown_de         0.386    
#> 4 euclid_de           0.0000159
#> 5 nugget              0.00242

Most of the variability in summer mean stream temperature is explained by the fixed effects of elevation and precipitation (Covariates (PR-sq)), the tail-up component, and the tail-down component. Note that the values in the proportion column sum to one.

In the remainder of this subsection, we describe the broom (Robinson, Hayes, and Couch 2021) functions tidy(), glance() and augment(). tidy() tidies coefficient output in a convenient tibble, glance() glances at model-fit statistics, and augment() augments the data with fitted model diagnostics.

We tidy the fixed effects (and add confidence intervals) by running

tidy(ssn_mod, conf.int = TRUE)

#> # A tibble: 3 × 7
#>   term        estimate std.error statistic  p.value conf.low   conf.high
#>   <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>       <dbl>
#> 1 (Intercept) 78.2      12.2          6.42 1.39e-10  54.3    102.       
#> 2 AREAWTMAP   -0.00807   0.00413     -1.96 5.05e- 2  -0.0162   0.0000187
#> 3 ELEV_DEM    -0.0288    0.00581     -4.95 7.35e- 7  -0.0401  -0.0174

We glance at the model-fit statistics by running

glance(ssn_mod)

#> # A tibble: 1 × 9
#>       n     p  npar value   AIC  AICc logLik deviance pseudo.r.squared
#>   <int> <dbl> <int> <dbl> <dbl> <dbl>  <dbl>    <dbl>            <dbl>
#> 1    45     3     7  76.6  90.6  93.7  -38.3     41.8            0.416

The columns of this tibble represent:

• n: The sample size.
• p: The number of fixed effects (linearly independent columns in \(\mathbf{X}\)).
• npar: The number of estimated covariance parameters.
• value: The value of the minimized objective function used when fitting the model.
• AIC: The Akaike Information Criterion (AIC).
• AICc: The AIC with a small sample size correction.
• logLik: The log-likelihood.
• deviance: The deviance.
• pseudo.r.squared: The pseudo r-squared.

The glances() function can be used to glance at multiple models at once. Suppose we wanted to compare the current model to a new model that omits the tail-up and Euclidean components. We do this using glances() by running

ssn_mod2 <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  taildown_type = "spherical"
)
glances(ssn_mod, ssn_mod2)

#> # A tibble: 2 × 10
#>   model        n     p  npar value   AIC  AICc logLik deviance pseudo.r.squared
#>   <chr>    <int> <dbl> <int> <dbl> <dbl> <dbl>  <dbl>    <dbl>            <dbl>
#> 1 ssn_mod     45     3     7  76.6  90.6  93.7  -38.3     41.8            0.416
#> 2 ssn_mod2    45     3     3 130.  136.  137.   -65.1     41.9            0.180

Often AIC and AICc are used for model selection, as they balance model fit and model simplicity. The lower AIC and AICc for the original model (ssn_mod) indicates it is a better fit to the data (than ssn_mod2). Outside of glance() and glances(), the functions AIC(), AICc(), logLik(), deviance(), and pseudoR2() are available to compute the relevant statistics. Note that additive is only required when the tail-up covariance is specified. We are able to compare AIC and AICc for these models fit using REML because we are only changing the covariance structure, not the fixed effects structure. To compare AIC and AICc for models with varying fixed effect and covariance structures, use ML. For example, we compare a model with and without elevation to assess its importance:

ml_mod <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  estmethod = "ml"
)
ml_mod2 <- ssn_lm(
  formula = Summer_mn ~ AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  estmethod = "ml"
)
glances(ml_mod, ml_mod2)

#> # A tibble: 2 × 10
#>   model       n     p  npar value   AIC  AICc logLik deviance pseudo.r.squared
#>   <chr>   <int> <dbl> <int> <dbl> <dbl> <dbl>  <dbl>    <dbl>            <dbl>
#> 1 ml_mod     45     3     7  60.2  80.2  86.7  -30.1     45.4           0.461 
#> 2 ml_mod2    45     2     7  72.9  90.9  96.0  -36.4     44.9           0.0237

Elevation seems important to model fit, as evidenced by the lower AIC. Erin E. Peterson and Ver Hoef (2010) describe a two-step model procedure for model selection based on AIC when comparing models with varying covariance and fixed structures. First, all covariance components are included (tail-up, tail-down, Euclidean, nugget) and fixed effects are compared using ML. Then using the model with the lowest AIC, refit using REML and compare models with varying combinations of covariance components. Finally, proceed with the model having the lowest AIC. Another approach is to compare a suite of models (having varying fixed effect and covariance components) using ML and then refit the best model using REML. Henceforth, we proceed with the REML models, ssn_mod and ssn_mod2.

Another way to compare model fits is leave-one-out cross validation available via the loocv() function. loocv() returns many model-fit statistics. One of these in the root-mean-squared-prediction error, which captures the typical absolute error associated with a prediction. We can compare the mean-squared-prediction error between ssn_mod, ssn_mod2:

loocv_mod <- loocv(ssn_mod)
loocv_mod$RMSPE

#> [1] 0.4800386

loocv_mod2 <- loocv(ssn_mod2)
loocv_mod2$RMSPE

#> [1] 0.8150308

ssn_mod is the better model with respect to AIC, AICc, and RMSPE and shortly we use it to return model diagnostics and make predictions. Note that model comparison using loocv() does not depend on the estimation method (ML vs REML).

We augment the data with model diagnostics by running

aug_ssn_mod <- augment(ssn_mod)
aug_ssn_mod

#> Simple feature collection with 45 features and 9 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -1530805 ymin: 920324.3 xmax: -1503079 ymax: 931036.6
#> Projected CRS: USA_Contiguous_Albers_Equal_Area_Conic
#> # A tibble: 45 × 10
#>    Summer_mn ELEV_DEM AREAWTMAP .fitted  .resid    .hat .cooksd .std.resid pid  
#>  *     <dbl>    <int>     <dbl>   <dbl>   <dbl>   <dbl>   <dbl>      <dbl> <chr>
#>  1      14.9     1947     1001.    14.1  0.770  0.0724  2.74e-3     0.337  1    
#>  2      14.7     1952     1001.    14.0  0.714  0.0569  4.49e-5    -0.0486 2    
#>  3      14.6     1958     1001.    13.8  0.776  0.0629  2.59e-3     0.352  3    
#>  4      15.2     1923     1007.    14.8  0.427  0.125   4.71e-2     1.06   4    
#>  5      14.5     1932     1007.    14.5 -0.0437 0.0359  3.43e-2    -1.69   5    
#>  6      15.3     1940     1009.    14.3  1.01   0.0220  3.29e-3     0.670  6    
#>  7      15.1     1940     1010.    14.3  0.797  0.0178  1.05e-4    -0.133  7    
#>  8      14.9     1945     1013.    14.1  0.833  0.00213 8.13e-5    -0.338  8    
#>  9      15.0     1948     1025.    13.9  1.06   0.0560  1.82e-4     0.0988 9    
#> 10      15.0     1950     1025.    13.9  1.15   0.0471  6.84e-3     0.660  10   
#> # ℹ 35 more rows
#> # ℹ 1 more variable: geometry <POINT [m]>

The columns of this tibble represent:

• Summer_mn: Summer mean stream temperature.
• ELEV_DEM: Elevation.
• AREAWTMAP: Precipitation.
• .fitted: The fitted values (the estimated mean given the explanatory variable values).
• .resid: The residuals (the response minus the fitted values).
• .hat: The leverage (hat) values.
• .cooksd: The Cook’s distance.
• .std.residuals: Standardized residuals.
• pid: The pid value.
• geometry: The spatial information in the sf object.

By default, augment() only returns the variables in the data used by the model. All variables from the original data are returned by setting drop = FALSE. We can write the augmented data to a geopackage by loading sf (which comes installed alongside SSN2) and running

library(sf)
st_write(aug_ssn_mod, paste0(tempdir(), "/aug_ssn_mod.gpkg"))

Many of the model diagnostics returned by augment() can be visualized by running using plot(). For example, we plot the fitted values against the standardized residuals by running

plot(ssn_mod, which = 1)

There are 6 total diagnostic plots (specified via the which argument) that return the same information returned from running plot() on an lm() object.

Prediction (Kriging)

Commonly a goal of a data analysis is to make predictions at unobserved locations. In spatial contexts, prediction is often called Kriging. Next we make summer mean stream temperature predictions at each location in the pred1km data in mf04p by running

predict(ssn_mod, newdata = "pred1km")

While augment() was previously used to augment the original data with model diagnostics, it can also be used to augment the newdata with predictions:

aug_preds <- augment(ssn_mod, newdata = "pred1km")
aug_preds[, ".fitted"]

#> Simple feature collection with 175 features and 1 field
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -1530631 ymin: 914920.7 xmax: -1500020 ymax: 933466.4
#> Projected CRS: USA_Contiguous_Albers_Equal_Area_Conic
#> # A tibble: 175 × 2
#>    .fitted            geometry
#>      <dbl>         <POINT [m]>
#>  1    14.7 (-1528406 928161.4)
#>  2    14.7 (-1528202 928821.1)
#>  3    14.9 (-1528173 929414.9)
#>  4    14.4 (-1530218 926538.7)
#>  5    14.5 (-1529466 926808.1)
#>  6    14.5 (-1520657 929871.1)
#>  7    15.0 (-1519866 930025.5)
#>  8    14.7 (-1521823 930124.7)
#>  9    14.9 (-1523183 930469.7)
#> 10    15.2 (-1523860 930665.8)
#> # ℹ 165 more rows

Here .fitted represents the predictions. Confidence intervals for the mean response or prediction intervals for the predicted response can be obtained by specifying the interval argument in predict() and augment(). By default, predict() and augment() compute 95% intervals, though this can be changed using the level argument. The arguments for predict() and augment() on ssn_lm() objects is slightly different than the same arguments for an lm() object – to learn more run help("predict.SSN2", "SSN2") or help("augment.SSN2", "SSN2").

We visualize these predictions (overlain onto the stream network) by running

ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = aug_preds, aes(color = .fitted), size = 2) +
  scale_color_viridis_c(limits = c(0, 17), option = "H") +
  theme_bw()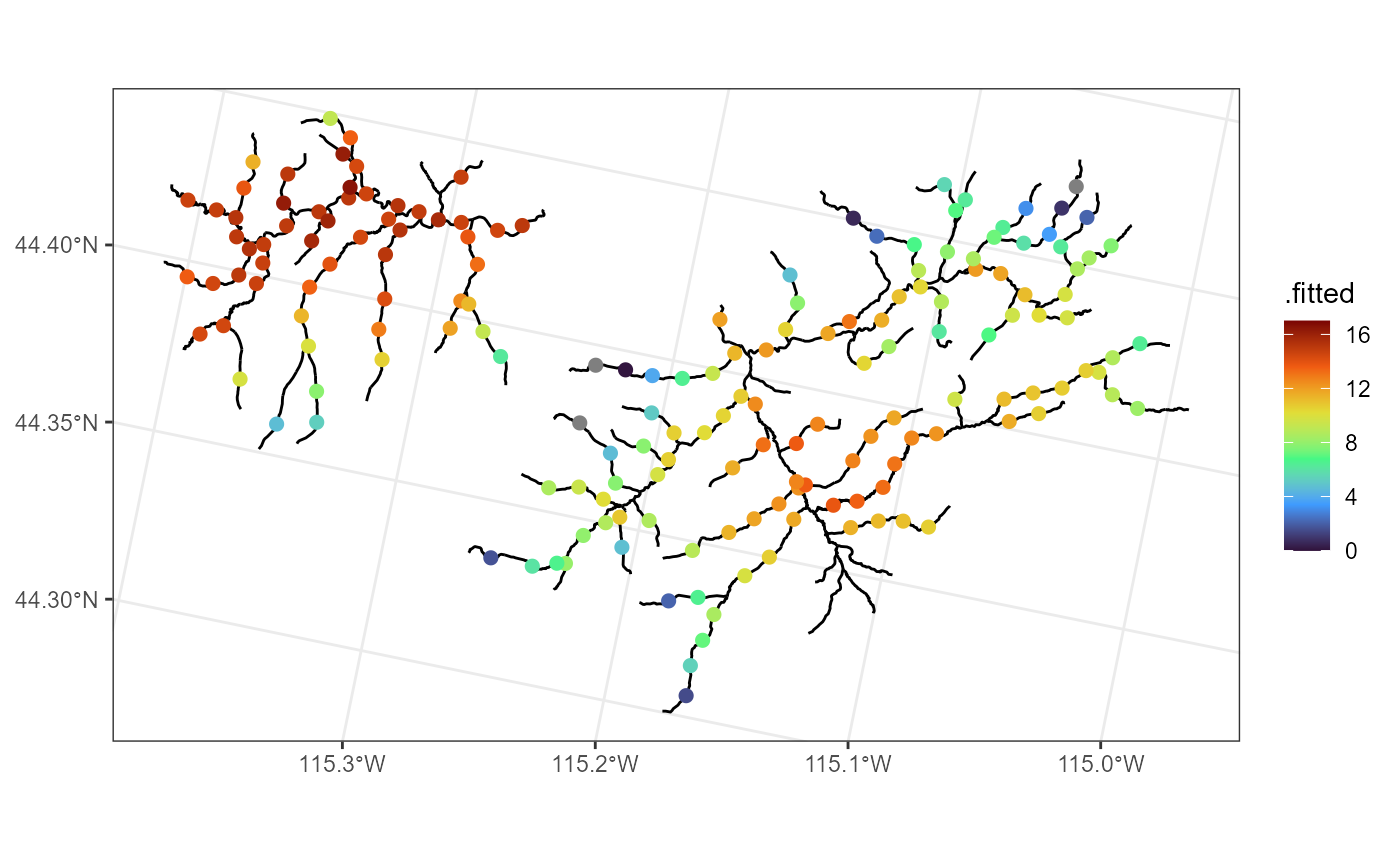

Previously we wrote out model diagnostics to a geopackage. Now we write out predictions to a geopackage (recall sf must be loaded) by running

st_write(aug_preds, paste0(tempdir(), "/aug_preds.gpkg"))

When performing prediction in SSN2, the name of newdata must be the name of a prediction data set contained in ssn.object$preds. If newdata is omitted or has the value "all", prediction is performed for all prediction data sets in ssn.object. For example,

predict(ssn_mod)
predict(ssn_mod, newdata = "all")

makes predictions for pred1km and CapeHorn (the names of mf04p$preds). Lastly, if there are observations (in the obs object) whose response is missing (NA), these observations are removed from model fitting and moved to a prediction data set named .missing. Then predictions can be obtained at these locations.

We can also predict the average value in a region using block Prediction (instead of making point predictions). We predict the average summer mean temperature throughout the Middle Fork stream network by running

predict(ssn_mod, newdata = "pred1km", block = TRUE, interval = "prediction")

#>        fit      lwr      upr
#> 1 10.21747 9.317693 11.11725

Advanced Features

There are several additional modeling tools available in SSN2 that we discuss next: Fixing parameter values; non-spatial random effects; and partition factors.

Perhaps we want to assume a particular covariance parameter is known. This may be reasonable if information is known about the process or the desire is to perform model selection for nested models or create profile likelihood confidence intervals. Fixing covariance parameters in SSN2 is accomplished via the tailup_initial, taildown_initial, euclid_initial, and nugget_initial arguments to ssn_lm(). These arguments are passed an appropriate initial value object created using the tailup_initial(), taildown_initial(), euclid_initial(), or nugget_initial() function, respectively. For example, suppose we want to fix the Euclidean dependent error variance parameter (i.e., Euclidean partial sill, or parsill) at 1, forcing this component to have a moderate effect on the covariance. First, we specify the appropriate object by running

euclid_init <- euclid_initial("gaussian", de = 1, known = "de")
euclid_init

#> $initial
#> de 
#>  1 
#> 
#> $is_known
#>   de 
#> TRUE 
#> 
#> attr(,"class")
#> [1] "euclid_gaussian"

The euclid_init output shows that the de parameter has an initial value of 1 that is assumed known. The range parameter will still be estimated. Next the model is fit:

ssn_init <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_initial = euclid_init,
  additive = "afvArea"
)
ssn_init

#> 
#> Call:
#> ssn_lm(formula = Summer_mn ~ ELEV_DEM + AREAWTMAP, ssn.object = mf04p, 
#>     tailup_type = "exponential", taildown_type = "spherical", 
#>     euclid_initial = euclid_init, additive = "afvArea")
#> 
#> 
#> Coefficients (fixed):
#> (Intercept)     ELEV_DEM    AREAWTMAP  
#>   71.247739    -0.026707    -0.005522  
#> 
#> Coefficients (covariance):
#>               Effect     Parameter   Estimate
#>   tailup exponential  de (parsill)  1.250e+00
#>   tailup exponential         range  4.191e+05
#>   taildown spherical  de (parsill)  1.924e-02
#>   taildown spherical         range  3.125e+04
#>      euclid gaussian  de (parsill)  1.000e+00
#>      euclid gaussian         range  9.998e+03
#>               nugget        nugget  3.578e-02

Random effects can be added to an SSN model to incorporate additional sources of variability separate from those on the stream network. Common additional sources of variability modeled include repeated observations at sites or network-specific effects. The random effects are modeled using similar syntax as for random effects in the nlme (Pinheiro and Bates 2006) and lme4 (Bates et al. 2015) R packages, being specified via a formula passed to the random argument. We model random intercepts for each of the two networks in the data by running

ssn_rand <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  random = ~ as.factor(netID)
)
ssn_rand

#> 
#> Call:
#> ssn_lm(formula = Summer_mn ~ ELEV_DEM + AREAWTMAP, ssn.object = mf04p, 
#>     tailup_type = "exponential", taildown_type = "spherical", 
#>     euclid_type = "gaussian", additive = "afvArea", random = ~as.factor(netID))
#> 
#> 
#> Coefficients (fixed):
#> (Intercept)     ELEV_DEM    AREAWTMAP  
#>   59.579720    -0.020328    -0.006484  
#> 
#> Coefficients (covariance):
#>               Effect             Parameter   Estimate
#>   tailup exponential          de (parsill)  1.128e+00
#>   tailup exponential                 range  2.015e+05
#>   taildown spherical          de (parsill)  2.948e-03
#>   taildown spherical                 range  8.357e+04
#>      euclid gaussian          de (parsill)  1.397e+00
#>      euclid gaussian                 range  1.096e+04
#>               nugget                nugget  2.977e-02
#>               random  1 | as.factor(netID)  4.370e+00

random = ~ as.factor(netID) is short-hand for random = ~ (1 | as.factor(netID)), which is the more familiar lme4 or nlme syntax.

A partition factor is a variable that allows observations to be uncorrelated when they do not share the same value. For example, one may want to partition the model into two networks (despite their adjacency) because of a significant land mass (or similar obstruction). In this case, it may be relevant to assume observations upstream of the land mass are not correlated with observations downstream of the land mass. Incorporating an effect as a partition factor is different from incorporating the effect as fixed (i.e., on the right-hand side of the formula argument). Partition factors affect the covariance portion of the model while fixed effects affect the mean portion.

Partition factors are modeled using a formula that contains a single variable passed to the partition_factor argument:

ssn_part <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  partition_factor = ~ as.factor(netID)
)
ssn_part

#> 
#> Call:
#> ssn_lm(formula = Summer_mn ~ ELEV_DEM + AREAWTMAP, ssn.object = mf04p, 
#>     tailup_type = "exponential", taildown_type = "spherical", 
#>     euclid_type = "gaussian", additive = "afvArea", partition_factor = ~as.factor(netID))
#> 
#> 
#> Coefficients (fixed):
#> (Intercept)     ELEV_DEM    AREAWTMAP  
#>   77.421289    -0.028431    -0.007938  
#> 
#> Coefficients (covariance):
#>               Effect     Parameter   Estimate
#>   tailup exponential  de (parsill)  1.331e+00
#>   tailup exponential         range  9.689e+05
#>   taildown spherical  de (parsill)  2.923e+00
#>   taildown spherical         range  1.880e+05
#>      euclid gaussian  de (parsill)  1.654e-04
#>      euclid gaussian         range  2.458e+01
#>               nugget        nugget  1.487e-02

Here, the partition factor ensures that observations from separate stream networks are completely uncorrelated.

Generalized Linear SSN Models

Generalized linear spatial stream network models for a response vector \(\mathbf{y}\) have spatially dependent random errors and are often parameterized as

\[\begin{equation*} g(\boldsymbol{\mu}) = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\tau}_{tu} + \boldsymbol{\tau}_{td} + \boldsymbol{\tau}_{eu} + \boldsymbol{\epsilon}, \end{equation*}\]

where \(\boldsymbol{\mu}\) is the mean of \(\mathbf{y}\), \(g(\cdot)\) is a link function that “links” \(\boldsymbol{\mu}\) to a linear function of the predictor variables and random errors, and all other terms are the same as those defined for linear spatial stream network models. Rather than assuming \(y\) is normally (Gaussian) distributed as is often the case with linear spatial stream network models, generalized linear spatial stream network models assume \(\mathbf{y}\) follows one of many distributions and has a corresponding link function. Below we summarize the families of generalized linear spatial stream network models supported by SSN2 their link functions, and the type of data typically associated with these families. For more on generalized linear models more generally, see McCullagh and Nelder (1989), Myers et al. (2012), and Faraway (2016).

The ssn_glm() function is used to fit generalized linear spatial stream network models and bears many similarities to base-R’s glm() function for non-spatial generalized linear models. The family (i.e., response distribution) is controlled by the family argument. When family is Gaussian(), the model fit is equivalent to one fit using ssn_lm(). Note that parameters are estimated on the relevant link scale and should be interpreted accordingly.

Family	Link Function	Link Name	Data Type	SSN2 Function
Gaussian	\(g(\mathbf{\mu}) = \mathbf{\mu}\)	Identity	Continuous	ssn_lm(); ssn_glm()
Binomial	\(g(\mathbf{\mu}) = \log(\mathbf{\mu} / (1 - \mathbf{\mu}))\)	Logit	Binary; Binary Count	ssn_glm()
Beta	\(g(\mathbf{\mu}) = \log(\mathbf{\mu} / (1 - \mathbf{\mu}))\)	Logit	Proportion	ssn_glm()
Poisson	\(g(\mathbf{\mu}) = \log(\mathbf{\mu})\)	Log	Count	ssn_glm()
Negative Binomial	\(g(\mathbf{\mu}) = \log(\mathbf{\mu})\)	Log	Count	ssn_glm()
Gamma	\(g(\mathbf{\mu}) = \log(\mathbf{\mu})\)	Log	Skewed (positive continuous)	ssn_glm()
Inverse Gaussian	\(g(\mathbf{\mu}) = \log(\mathbf{\mu})\)	Log	Skewed (positive continuous)	ssn_glm()

The C16 variable in mf04p represents the number of times daily summer stream temperature exceeded 16 Celsius:

ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = mf04p$obs, aes(color = C16), size = 2) +
  scale_color_viridis_c(option = "H") +
  theme_bw()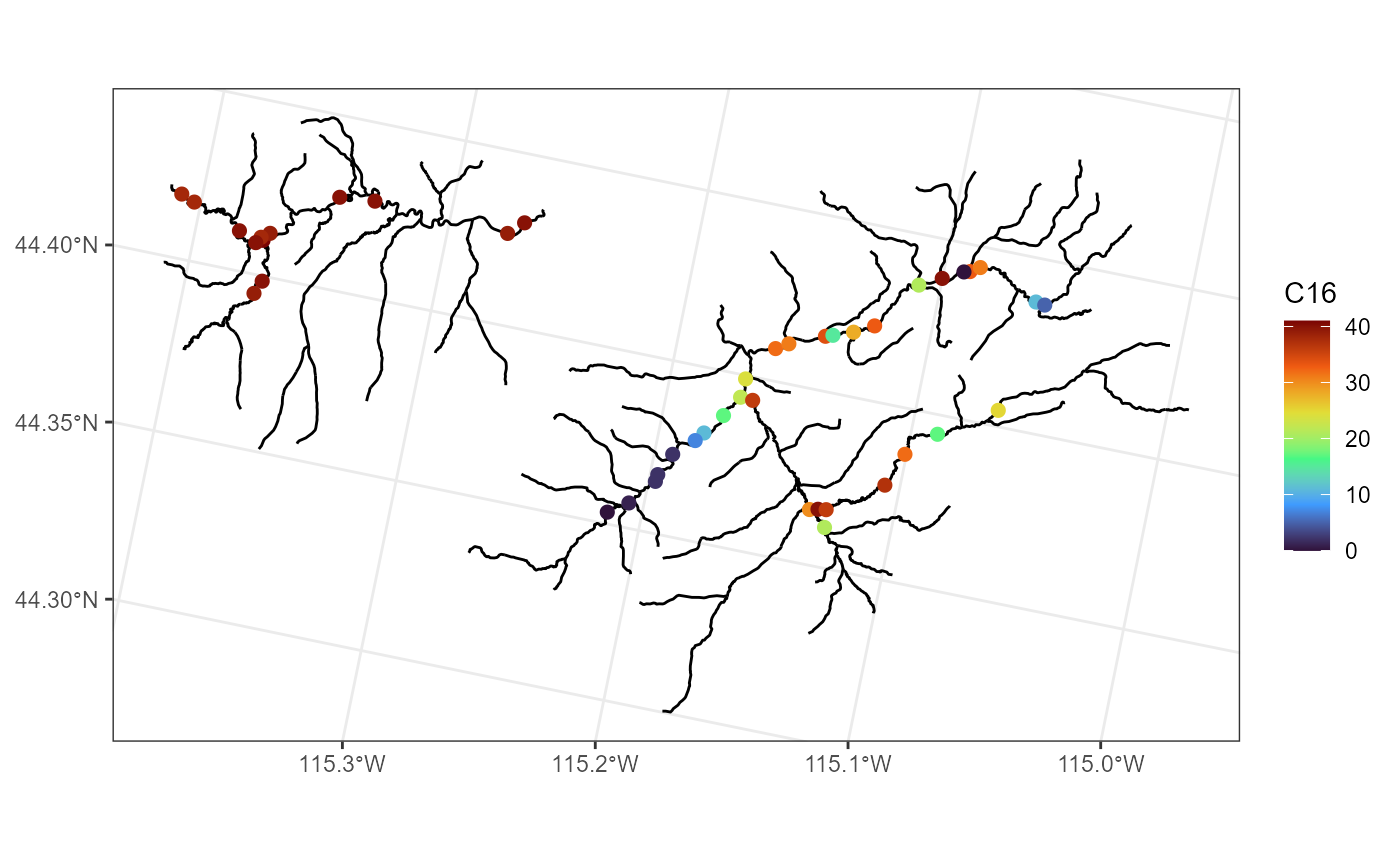

Suppose we want to model C16 as a function of elevation and precipitation. Often count data are modeled using Poisson regression. Using tail-up, tail-down, and nugget components, we fit this Poisson model by running

ssn_pois <- ssn_glm(
  formula = C16 ~ ELEV_DEM + AREAWTMAP,
  family = "poisson",
  ssn.object = mf04p,
  tailup_type = "epa",
  taildown_type = "mariah",
  additive = "afvArea"
)

The previous SSN2 functions used to explore linear spatial stream network models are also available for generalized linear spatial stream network models. For example, we can summarize the model using summary():

summary(ssn_pois)

#> 
#> Call:
#> ssn_glm(formula = C16 ~ ELEV_DEM + AREAWTMAP, ssn.object = mf04p, 
#>     family = "poisson", tailup_type = "epa", taildown_type = "mariah", 
#>     additive = "afvArea")
#> 
#> Deviance Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -3.10387 -0.36874 -0.05467  0.27401  1.37106 
#> 
#> Coefficients (fixed):
#>              Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) 45.889749   9.803696   4.681 2.86e-06 ***
#> ELEV_DEM    -0.018206   0.004547  -4.004 6.24e-05 ***
#> AREAWTMAP   -0.006715   0.002958  -2.270   0.0232 *  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Pseudo R-squared: 0.2527
#> 
#> Coefficients (covariance):
#>            Effect     Parameter   Estimate
#>        tailup epa  de (parsill)  6.358e-01
#>        tailup epa         range  3.090e+04
#>   taildown mariah  de (parsill)  7.500e-02
#>   taildown mariah         range  2.878e+06
#>            nugget        nugget  1.289e-03
#>        dispersion    dispersion  1.000e+00

Similar to summaries of glm() objects, summaries of ssn_glm() objects include the original function call, deviance residuals, and a coefficients table of fixed effects. The (Intercept) represents the log average C16 at sea level (an elevation of zero) and zero precipitation, ELEV_DEM represents the decrease in log average summer mean temperature with a one unit (meter) increase in elevation, and AREAWTMAP represents the decrease in log average summer mean temperature with a one unit (mm) increase in precipitation. There is strong evidence that log average summer mean temperature decreases with elevation (\(p\)-value \(< 0.001\)), while there is moderate evidence that log average summer mean temperature decreases with precipitation (\(p\)-value \(\approx\) 0.03). Recall that the covariance parameter estimates are on the link (here, log) scale.

The Poisson model assumes that each observations mean and variance are equal. Often with ecological or environmental data, the variance is larger than the mean – this is called overdispersion. The negative binomial model accommodates overdispersion for count data. We fit a negative binomial model by running

ssn_nb <- ssn_glm(
  formula = C16 ~ ELEV_DEM + AREAWTMAP,
  family = "nbinomial",
  ssn.object = mf04p,
  tailup_type = "epa",
  taildown_type = "mariah",
  additive = "afvArea"
)

We can compare the fit of these models using leave-one-out cross validation by running

loocv_pois <- loocv(ssn_pois)
loocv_pois$RMSPE

#> [1] 6.015313

loocv_nb <- loocv(ssn_nb)
loocv_nb$RMSPE

#> [1] 5.875028

The negative binomial model has a lower RMSPE, which suggests some evidence of overdispersion. Other ways to assess the impact of overdispersion include 1) comparing the models using a likelihood-based fit statistic like AIC; if the AIC values are similar there is little evidence of overdispersion – and 2) inspecting the dispersion parameter estimates of the negative binomial model; if the dispersion parameter is very large, there is little evidence of overdispersion.

All advanced modeling features discussed for linear spatial stream network models (e.g., fixing covariance parameter values, random effects, partition factors) are also available for generalized linear spatial stream network models.

Simulating Spatial Stream Network Data

The ssn_simulate() function is used to simulate data on a stream network. First, covariance parameter values are specified and a seed set:

tu_params <- tailup_params("exponential", de = 0.4, range = 1e5)
td_params <- taildown_params("spherical", de = 0.1, range = 1e6)
euc_params <- euclid_params("gaussian", de = 0.2, range = 1e3)
nug_params <- nugget_params("nugget", nugget = 0.1)
set.seed(2)

Then call ssn_simulate(), specifying the family argument depending on the type of simulated data desired (here, Gaussian), the ssn.object and the network (here, the observed network):

sims <- ssn_simulate(
  family = "gaussian",
  ssn.object = mf04p,
  network = "obs",
  additive = "afvArea",
  tailup_params = tu_params,
  taildown_params = td_params,
  euclid_params = euc_params,
  nugget_params = nug_params,
  mean = 0,
  samples = 1
)
head(sims)

#> [1] -0.8022248 -0.4047795  0.3819883 -1.0798647 -0.8943244 -0.4111767

We simulate binomial (presence/absence) data by running

sims <- ssn_simulate(
  family = "binomial",
  ssn.object = mf04p,
  network = "obs",
  additive = "afvArea",
  tailup_params = tu_params,
  taildown_params = td_params,
  euclid_params = euc_params,
  nugget_params = nug_params,
  mean = 0,
  samples = 2
)
head(sims)

#>      1 2
#> [1,] 0 1
#> [2,] 0 1
#> [3,] 0 1
#> [4,] 1 1
#> [5,] 1 0
#> [6,] 0 0

Currently, ssn_simulate() only works on the observed network (network = "obs"). However, simulation in SSN2 will be a focus of future updates, and we plan to add support for simulating on prediction networks as well as observed and prediction networks simultaneously.

Function Glossary

Here we list the two SSN2 functions used to fit models:

• ssn_glm(): Fit a spatial stream network generalized linear model.
• ssn_lm(): Fit a spatial stream network linear model.

Here we list some commonly used SSN2 functions that operate on model fits:

• AIC(): Compute the AIC.
• AICc(): Compute the AICc.
• anova(): Perform an analysis of variance.
• augment(): Augment data with diagnostics or new data with predictions.
• coef(): Return coefficients.
• confint(): Compute confidence intervals.
• cooks.distance(): Compute Cook’s distance.
• covmatrix(): Return covariance matrices.
• deviance(): Compute the deviance.
• fitted(): Compute fitted values.
• glance(): Glance at a fitted model.
• glances(): Glance at multiple fitted models.
• hatvalues(): Compute leverage (hat) values.
• logLik(): Compute the log-likelihood.
• loocv(): Perform leave-one-out cross validation and compute relevant statistics.
• model.matrix(): Return the model matrix (\(\mathbf{X}\)).
• plot(): Create fitted model plots.
• predict(): Compute predictions and prediction intervals.
• pseudoR2(): Compute the pseudo r-squared.
• residuals(): Compute residuals.
• summary(): Summarize fitted models.
• tidy(): Tidy fitted models.
• varcomp(): Compare variance components.
• vcov(): Compute variance-covariance matrices of estimated parameters.

Documentation for these functions can be found by running ?function_name.SSN2 or help("function_name.SSN2", "SSN2"). For example, ?predict.SSN2 or help("predict.SSN2", "SSN2").

Here we list some commonly used SSN2 functions for manipulating SSN objects:

• ssn_create_distmat(): Create distance matrices in the .ssn directory for use with modeling functions.
• ssn_get_data(): Extract an sf data.frame of observed or prediction locations from the SSN object.
• ssn_get_netgeom(): Extract topological information from the netgeom column.
• ssn_get_stream_distmat(): Extract the stream distance matrices for the observed or prediction locations in an SSN object.
• ssn_import(): Import an SSN object from an .ssn directory.
• ssn_import_predpts(): Import prediction data and store within an existing SSN object.
• ssn_put_data(): Replace an sf data.frame of observed or prediction locations in an SSN object.
• ssn_split_predpts(): Split prediction data stored within an SSN object into multiple prediction data sets.
• ssn_subset(): Subset an existing SSN object based on a logical expression.
• SSN_to_SSN2(): Convert an S4 SpatialStreamNetwork object created in the SSN to an S3 SSN object used in SSN2.
• ssn_update_path(): Update the path element of an SSN object.
• ssn_write(): Write an SSN project to a new local .ssn directory.

All functions that manipulate SSN objects have an ssn_ prefix, which makes them easily accessible via tab completion in RStudio.

Here we list some commonly used miscellaneous SSN2 functions:

• ssn_simulate(): Simulate spatially autocorrelated random variables on a stream network.

For a full list of SSN2 functions alongside their documentation, see the documentation manual.

From SSN to SSN2

Here we present a table of SSN functions and provide their relevant successors in SSN2:

SSN Function Name	SSN2 Function Name
AIC()	AIC(); AICc()
BlockPredict()	predict(…, block = TRUE)
BLUP()	fitted(…, type)
covparms()	coef(); tidy(..., effects)
createDistMat()	ssn_create_distmat()
CrossValidationSSN()	loocv()
CrossValidationStatsSSN()	loocv()
EmpiricalSemivariogram()	Torgegram(…, type)
getSSNdata.frame()	ssn_get_data()
getStreamDistMat()	ssn_get_stream_distmat()
glmssn()	ssn_glm(); ssn_lm()
GR2()	pseudoR2()
importPredpts()	ssn_import_predpts()
importSSN()	ssn_import()
InfoCritCompare()	augment(); glance(); glances(); loocv()
predict()	predict()
putSSNdata.frame()	ssn_put_data()
residuals()	residuals()
SimulateOnSSN()	ssn_simulate()
splitPredictions()	ssn_split_predpts()
subsetSSN()	ssn_subset()
summary()	summary()
Torgegram()	Torgegram(…, type)
updatePath()	ssn_update_path()
varcomp()	varcomp()
writeSSN()	ssn_write()

In addition to the function name changes above, a few function argument names also changed. Please read the documentation for each function of interest to see its relevant argument name changes.

The Future of SSN2

There are several features we have planned for future versions of SSN2 that did not make it into the initial release due to the October timeline regarding the rgdal, rgeos, and maptools retirements. As such, we plan to regularly update and add features to SSN2 in the coming years – so check back often! Some of these features include additional tools for large data sets (both model fitting and prediction), manipulating the .ssn object, simulating data, and more. We will do our best to make future versions of SSN2 backward compatible with this version, but minor changes may occur until we are ready to release version 1.0.0.

R Code Appendix

library(SSN2)
citation(package = "SSN2")
path <- system.file("lsndata/MiddleFork04.ssn", package = "SSN2")
copy_lsn_to_temp()
path <- file.path(tempdir(), "MiddleFork04.ssn")
mf04p <- ssn_import(
  path = path,
  predpts = c("pred1km", "CapeHorn"),
  overwrite = TRUE
)
summary(mf04p)
library(ggplot2)
names(mf04p$preds)
ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = mf04p$preds$pred1km, pch = 17, color = "blue") +
  geom_sf(data = mf04p$obs, color = "brown", size = 2) +
  theme_bw()
ssn_create_distmat(
  ssn.object = mf04p,
  predpts = c("pred1km", "CapeHorn"),
  among_predpts = TRUE,
  overwrite = TRUE
)
ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = mf04p$obs, aes(color = Summer_mn), size = 2) +
  scale_color_viridis_c(limits = c(0, 17), option = "H") +
  theme_bw()
tg <- Torgegram(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  type = c("flowcon", "flowuncon", "euclid")
)
plot(tg)
ssn_mod <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea"
)
summary(ssn_mod)
varcomp(ssn_mod)
tidy(ssn_mod, conf.int = TRUE)
glance(ssn_mod)
ssn_mod2 <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  taildown_type = "spherical"
)
glances(ssn_mod, ssn_mod2)
ml_mod <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  estmethod = "ml"
)
ml_mod2 <- ssn_lm(
  formula = Summer_mn ~ AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  estmethod = "ml"
)
glances(ml_mod, ml_mod2)
loocv_mod <- loocv(ssn_mod)
loocv_mod$RMSPE
loocv_mod2 <- loocv(ssn_mod2)
loocv_mod2$RMSPE
aug_ssn_mod <- augment(ssn_mod)
aug_ssn_mod
library(sf)
st_write(aug_ssn_mod, paste0(tempdir(), "/aug_ssn_mod.gpkg"))
plot(ssn_mod, which = 1)
predict(ssn_mod, newdata = "pred1km")
aug_preds <- augment(ssn_mod, newdata = "pred1km")
aug_preds[, ".fitted"]
ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = aug_preds, aes(color = .fitted), size = 2) +
  scale_color_viridis_c(limits = c(0, 17), option = "H") +
  theme_bw()
st_write(aug_preds, paste0(tempdir(), "/aug_preds.gpkg"))
predict(ssn_mod)
predict(ssn_mod, newdata = "all")
predict(ssn_mod, newdata = "pred1km", block = TRUE, interval = "prediction")
euclid_init <- euclid_initial("gaussian", de = 1, known = "de")
euclid_init
ssn_init <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_initial = euclid_init,
  additive = "afvArea"
)
ssn_init
ssn_rand <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  random = ~ as.factor(netID)
)
ssn_rand
ssn_part <- ssn_lm(
  formula = Summer_mn ~ ELEV_DEM + AREAWTMAP,
  ssn.object = mf04p,
  tailup_type = "exponential",
  taildown_type = "spherical",
  euclid_type = "gaussian",
  additive = "afvArea",
  partition_factor = ~ as.factor(netID)
)
ssn_part
ggplot() +
  geom_sf(data = mf04p$edges) +
  geom_sf(data = mf04p$obs, aes(color = C16), size = 2) +
  scale_color_viridis_c(option = "H") +
  theme_bw()
ssn_pois <- ssn_glm(
  formula = C16 ~ ELEV_DEM + AREAWTMAP,
  family = "poisson",
  ssn.object = mf04p,
  tailup_type = "epa",
  taildown_type = "mariah",
  additive = "afvArea"
)
summary(ssn_pois)
ssn_nb <- ssn_glm(
  formula = C16 ~ ELEV_DEM + AREAWTMAP,
  family = "nbinomial",
  ssn.object = mf04p,
  tailup_type = "epa",
  taildown_type = "mariah",
  additive = "afvArea"
)
loocv_pois <- loocv(ssn_pois)
loocv_pois$RMSPE
loocv_nb <- loocv(ssn_nb)
loocv_nb$RMSPE
tu_params <- tailup_params("exponential", de = 0.4, range = 1e5)
td_params <- taildown_params("spherical", de = 0.1, range = 1e6)
euc_params <- euclid_params("gaussian", de = 0.2, range = 1e3)
nug_params <- nugget_params("nugget", nugget = 0.1)
set.seed(2)
sims <- ssn_simulate(
  family = "gaussian",
  ssn.object = mf04p,
  network = "obs",
  additive = "afvArea",
  tailup_params = tu_params,
  taildown_params = td_params,
  euclid_params = euc_params,
  nugget_params = nug_params,
  mean = 0,
  samples = 1
)
head(sims)
sims <- ssn_simulate(
  family = "binomial",
  ssn.object = mf04p,
  network = "obs",
  additive = "afvArea",
  tailup_params = tu_params,
  taildown_params = td_params,
  euclid_params = euc_params,
  nugget_params = nug_params,
  mean = 0,
  samples = 2
)
head(sims)

References

Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015. “Fitting Linear Mixed-Effects Models Using lme4.” Journal of Statistical Software 67 (1): 1–48. https://doi.org/10.18637/jss.v067.i01.

Bivand, Roger, Tim Keitt, and Barry Rowlingson. 2021. Rgdal: Bindings for the ’Geospatial’ Data Abstraction Library. https://CRAN.R-project.org/package=rgdal.

Bivand, Roger, and Nicholas Lewin-Koh. 2021. Maptools: Tools for Handling Spatial Objects. https://CRAN.R-project.org/package=maptools.

Bivand, Roger, and Colin Rundel. 2020. Rgeos: Interface to Geometry Engine - Open Source (’GEOS’). https://CRAN.R-project.org/package=rgeos.

Cressie, Noel, Jesse Frey, Bronwyn Harch, and Mick Smith. 2006. “Spatial Prediction on a River Network.” Journal of Agricultural, Biological, and Environmental Statistics 11: 127–50.

Dumelle, Michael, Matt Higham, and Jay M Ver Hoef. 2023. “Spmodel: Spatial Statistical Modeling and Prediction in r.” Plos One 18 (3): e0282524.

Faraway, Julian J. 2016. Extending the Linear Model with r: Generalized Linear, Mixed Effects and Nonparametric Regression Models. Chapman; Hall/CRC.

Isaak, Daniel J, Erin E Peterson, Jay M Ver Hoef, Seth J Wenger, Jeffrey A Falke, Christian E Torgersen, Colin Sowder, et al. 2014. “Applications of Spatial Statistical Network Models to Stream Data.” Wiley Interdisciplinary Reviews: Water 1 (3): 277–94.

McCullagh, Peter, and John A Nelder. 1989. Generalized Linear Models, 2nd Edition. Chapman & Hall Ltd.

Myers, Raymond H, Douglas C Montgomery, G Geoffrey Vining, and Timothy J Robinson. 2012. Generalized Linear Models: With Applications in Engineering and the Sciences. John Wiley & Sons.

Nowosad, Jakub. 2023. “Upcoming Changes to Popular R Packages for Spatial Data: What You Need to Do.” June 4, 2023. https://geocompx.org//post/2023/rgdal-retirement.

Pebesma, Edzer. 2018. “Simple Features for R: Standardized Support for Spatial Vector Data.” The R Journal 10 (1): 439–46. https://doi.org/10.32614/RJ-2018-009.

Peterson, Erin E., Michael Dumelle, Alan Pearse, Dan Teleki, and Jay M. Ver Hoef. 2024. SSNbler: Assemble SSN Objects in R. https://github.com/pet221/SSNbler.

Peterson, Erin E., Jay M. Ver Hoef, Dan J. Isaak, Jeffrey A. Falke, Marie-Jose Fortin, Chris E. Jordan, Kristina McNyset, et al. 2013. “Modelling Dendritic Ecological Networks in Space: An Integrated Network Perspective.” Ecology Letters 16 (5): 707–19.

Peterson, Erin E, and Jay M Ver Hoef. 2010. “A Mixed-Model Moving-Average Approach to Geostatistical Modeling in Stream Networks.” Ecology 91 (3): 644–51.

Peterson, Erin, and Jay Ver Hoef. 2014. “STARS: An ArcGIS Toolset Used to Calculate the Spatial Information Needed to Fit Spatial Statistical Models to Stream Network Data.” Journal of Statistical Software 56: 1–17.

Pinheiro, José, and Douglas Bates. 2006. Mixed-Effects Models in s and s-PLUS. Springer science & business media.

Robinson, David, Alex Hayes, and Simon Couch. 2021. Broom: Convert Statistical Objects into Tidy Tibbles. https://CRAN.R-project.org/package=broom.

Ver Hoef, Jay M, and Erin E Peterson. 2010. “A Moving Average Approach for Spatial Statistical Models of Stream Networks.” Journal of the American Statistical Association 105 (489): 6–18.

Ver Hoef, Jay M, Erin Peterson, and David Theobald. 2006. “Spatial Statistical Models That Use Flow and Stream Distance.” Environmental and Ecological Statistics.

Ver Hoef, Jay, Erin Peterson, David Clifford, and Rohan Shah. 2014. “SSN: An R Package for Spatial Statistical Modeling on Stream Networks.” Journal of Statistical Software 56: 1–45.

Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org.

Zimmerman, Dale L, and Jay M Ver Hoef. 2017. “The Torgegram for Fluvial Variography: Characterizing Spatial Dependence on Stream Networks.” Journal of Computational and Graphical Statistics 26 (2): 253–64.