Compute the empirical autocovariance

Compute the empirical autocovariance (i.e., empirical covariance) for varying bin sizes and cutoff values.

eacf(
  formula,
  data,
  xcoord,
  ycoord,
  cloud = FALSE,
  bins = 15,
  cutoff,
  dist_matrix,
  partition_factor
)

# S3 method for eacf
plot(x, ...)

Arguments

formula: A formula describing the fixed effect structure.
data: A data frame or sf object containing the variables in formula and geographic information.
xcoord: Name of the variable in data representing the x-coordinate. Can be quoted or unquoted. Not required if data is an sf object.
ycoord: Name of the variable in data representing the y-coordinate. Can be quoted or unquoted. Not required if data is an sf object.
cloud: A logical indicating whether the empirical autocovariance should be summarized by distance class or not. When cloud = FALSE (the default), pairwise autocovariances are binned and averaged within distance classes. When cloud = TRUE, all pairwise autocovariances and distances are returned (this is known as the "cloud" autocovariance).
bins: The number of equally spaced bins. The default is 15. Ignored if cloud = TRUE.
cutoff: The maximum distance considered. The default is half the diagonal of the bounding box from the coordinates.
dist_matrix: A distance matrix to be used instead of providing coordinate names.
partition_factor: An optional formula specifying the partition factor. If specified, autocovariances are only computed for observations sharing the same level of the partition factor.
x: An object from eacf().
...: Other arguments passed to other methods.

Value

If cloud = FALSE, a tibble (data.frame) with distance bins (bins), the average distance (dist), the average autocovariance (acov), and the number of (unique) pairs (np). If cloud = TRUE, a tibble (data.frame) with distance (dist) and autocovariance (acov) for each unique pair.

Details

The empirical autocovariance (i.e., empirical covariance) is a tool used to visualize and model spatial dependence by estimating the semivariance of a process at varying distances. For a constant-mean process, the autocovariance at distance \(h\) is denoted \(Cov(h)\) and defined as \(Cov(z1, z2)\). Under second-order stationarity, \(Cov(h) = Cov(0) - \gamma(h)\), where \(gamma(h)\) is the semivariance function at distance h. Typically the residuals from an ordinary least squares fit defined by formula are second-order stationary with mean zero. These residuals are used to compute the empirical autocovariance At a distance h, the empirical autocovariance is \(1/N(h) \sum (r1 \times r2)\), where \(N(h)\) is the number of (unique) pairs in the set of observations whose distance separation is h and r1 and r2 are residuals corresponding to observations whose distance separation is h. In spmodel, these distance bins actually contain observations whose distance separation is h +- c, where c is a constant determined implicitly by bins. Typically, only observations whose distance separation is below some cutoff are used to compute the empirical semivariogram (this cutoff is determined by cutoff).

Examples

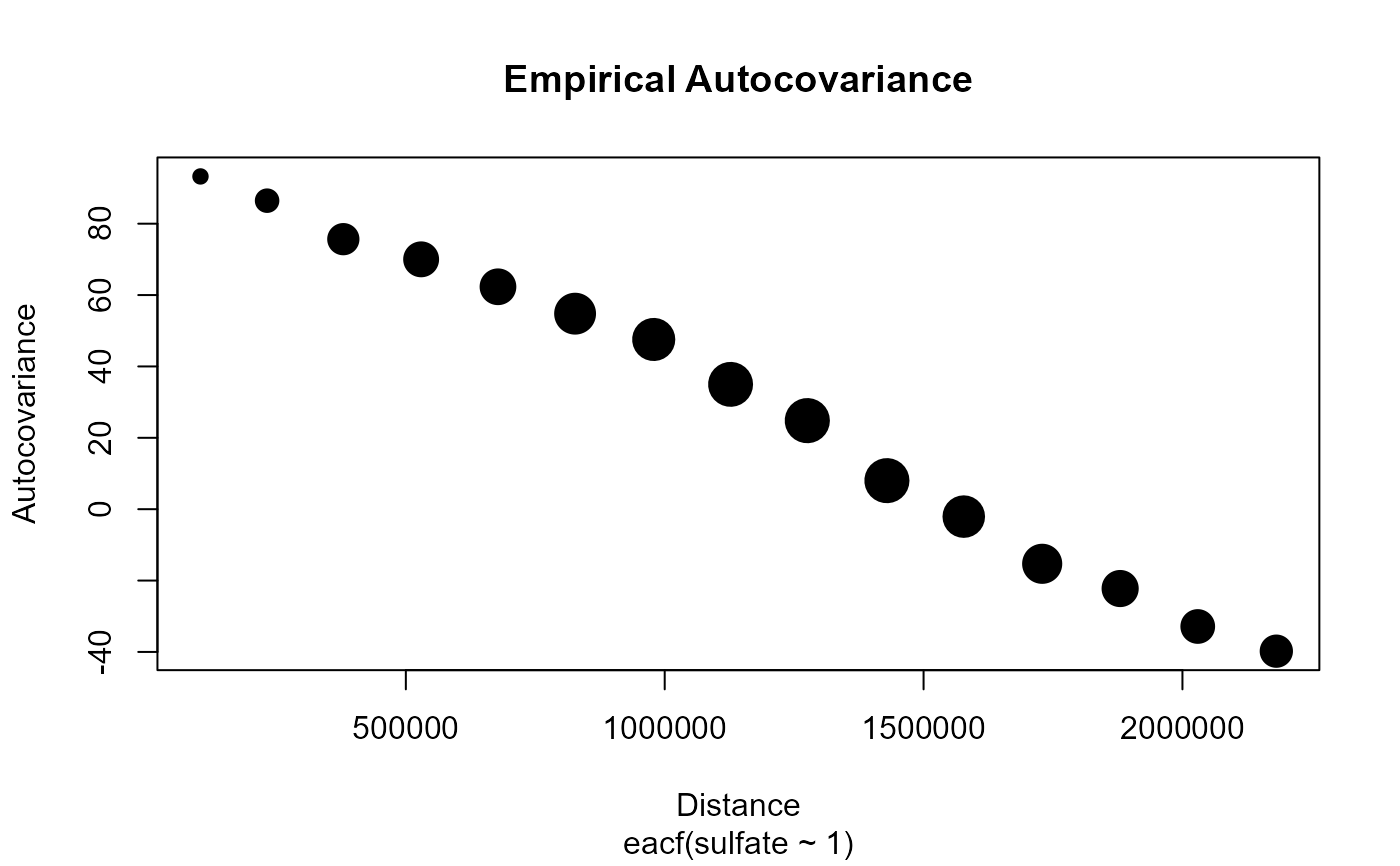
eacf(sulfate ~ 1, sulfate)
#> # A tibble: 15 × 4
#>    bins                    dist   acov    np
#>  * <fct>                  <dbl>  <dbl> <dbl>
#>  1 (0,1.5e+05]          103340.  93.2    149
#>  2 (1.5e+05,3.01e+05]   232014.  86.4    456
#>  3 (3.01e+05,4.51e+05]  379255.  75.7    749
#>  4 (4.51e+05,6.02e+05]  529543.  70.0    887
#>  5 (6.02e+05,7.52e+05]  677949.  62.3    918
#>  6 (7.52e+05,9.03e+05]  826917.  54.8   1113
#>  7 (9.03e+05,1.05e+06]  978773.  47.6   1161
#>  8 (1.05e+06,1.2e+06]  1127232.  35.0   1230
#>  9 (1.2e+06,1.35e+06]  1275415.  24.8   1239
#> 10 (1.35e+06,1.5e+06]  1429184.   8.00  1236
#> 11 (1.5e+06,1.65e+06]  1577636.  -2.08  1139
#> 12 (1.65e+06,1.81e+06] 1729098. -15.3   1047
#> 13 (1.81e+06,1.96e+06] 1879679. -22.2    934
#> 14 (1.96e+06,2.11e+06] 2029566. -32.9    842
#> 15 (2.11e+06,2.26e+06] 2181337. -39.8    788
plot(eacf(sulfate ~ 1, sulfate))