Compute the empirical semivariogram

Compute the empirical semivariogram for varying bin sizes and cutoff values.

esv(
  formula,
  data,
  xcoord,
  ycoord,
  cloud = FALSE,
  bins = 15,
  cutoff,
  dist_matrix,
  partition_factor
)

# S3 method for esv
plot(x, ...)

Arguments

formula: A formula describing the fixed effect structure.
data: A data frame or sf object containing the variables in formula and geographic information.
xcoord: Name of the variable in data representing the x-coordinate. Can be quoted or unquoted. Not required if data is an sf object.
ycoord: Name of the variable in data representing the y-coordinate. Can be quoted or unquoted. Not required if data is an sf object.
cloud: A logical indicating whether the empirical semivariogram should be summarized by distance class or not. When cloud = FALSE (the default), pairwise semivariances are binned and averaged within distance classes. When cloud = TRUE, all pairwise semivariances and distances are returned (this is known as the "cloud" semivariogram).
bins: The number of equally spaced bins. The default is 15. Ignored if cloud = TRUE.
cutoff: The maximum distance considered. The default is half the diagonal of the bounding box from the coordinates.
dist_matrix: A distance matrix to be used instead of providing coordinate names.
partition_factor: An optional formula specifying the partition factor. If specified, semivariances are only computed for observations sharing the same level of the partition factor.
x: An object from esv().
...: Other arguments passed to other methods.

Value

If cloud = FALSE, a tibble (data.frame) with distance bins (bins), the average distance (dist), the average semivariance (gamma), and the number of (unique) pairs (np). If cloud = TRUE, a tibble (data.frame) with distance (dist) and semivariance (gamma) for each unique pair.

Details

The empirical semivariogram is a tool used to visualize and model spatial dependence by estimating the semivariance of a process at varying distances. For a constant-mean process, the semivariance at distance \(h\) is denoted \(\gamma(h)\) and defined as \(0.5 * Var(z1 - z2)\). Under second-order stationarity, \(\gamma(h) = Cov(0) - Cov(h)\), where \(Cov(h)\) is the covariance function at distance h. Typically the residuals from an ordinary least squares fit defined by formula are second-order stationary with mean zero. These residuals are used to compute the empirical semivariogram. At a distance h, the empirical semivariance is \(1/N(h) \sum (r1 - r2)^2\), where \(N(h)\) is the number of (unique) pairs in the set of observations whose distance separation is h and r1 and r2 are residuals corresponding to observations whose distance separation is h. In spmodel, these distance bins actually contain observations whose distance separation is h +- c, where c is a constant determined implicitly by bins. Typically, only observations whose distance separation is below some cutoff are used to compute the empirical semivariogram (this cutoff is determined by cutoff).

When using splm() with estmethod as "sv-wls", the empirical semivariogram is calculated internally and used to estimate spatial covariance parameters.

Examples

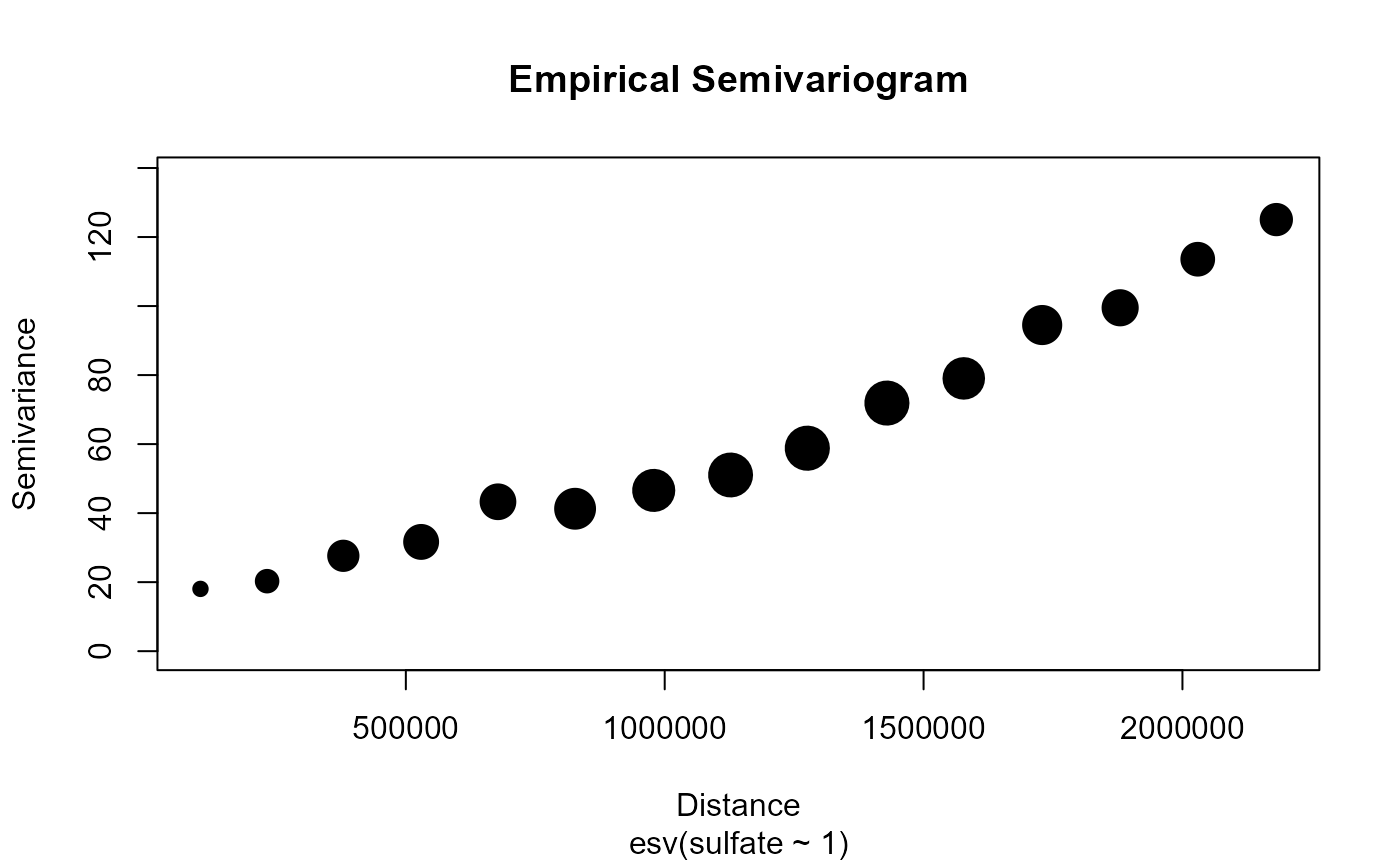
esv(sulfate ~ 1, sulfate)
#> # A tibble: 15 × 4
#>    bins                    dist gamma    np
#>  * <fct>                  <dbl> <dbl> <dbl>
#>  1 (0,1.5e+05]          103340.  18.0   149
#>  2 (1.5e+05,3.01e+05]   232014.  20.3   456
#>  3 (3.01e+05,4.51e+05]  379255.  27.6   749
#>  4 (4.51e+05,6.02e+05]  529543.  31.7   887
#>  5 (6.02e+05,7.52e+05]  677949.  43.3   918
#>  6 (7.52e+05,9.03e+05]  826917.  41.3  1113
#>  7 (9.03e+05,1.05e+06]  978773.  46.6  1161
#>  8 (1.05e+06,1.2e+06]  1127232.  51.1  1230
#>  9 (1.2e+06,1.35e+06]  1275415.  58.8  1239
#> 10 (1.35e+06,1.5e+06]  1429184.  71.9  1236
#> 11 (1.5e+06,1.65e+06]  1577636.  79.0  1139
#> 12 (1.65e+06,1.81e+06] 1729098.  94.5  1047
#> 13 (1.81e+06,1.96e+06] 1879679.  99.5   934
#> 14 (1.96e+06,2.11e+06] 2029566. 114.    842
#> 15 (2.11e+06,2.26e+06] 2181337. 125.    788
plot(esv(sulfate ~ 1, sulfate))