Recommendation logic¶
A BMDS session has a set of automated rules for recommending a best-fitting model from runs included in the session. The rules are a combination of heuristic and statistical rules, and were generated from two sources:
USEPA BMDS technical guidance (EPA 2012)
When configuring a session, a user selects which models and model recommendations are enabled. If enabled, the recommendation logic has reasonable defaults, but you can also manually configure the logic by turning on/off individual checks and threshold values. Results are extracted from model outputs, and models are placed into one of three possible bins, depending on the results and the bin recommendation logic:
Failure: model did not successfully complete
Nonviable model: model successfully completed, but there are serious issues
Viable model: candidate for recommended model, but there may be warnings
If at least one viable model exists, then it may be selected as a best-fitting model. This would be consistent with the workflow diagram below:
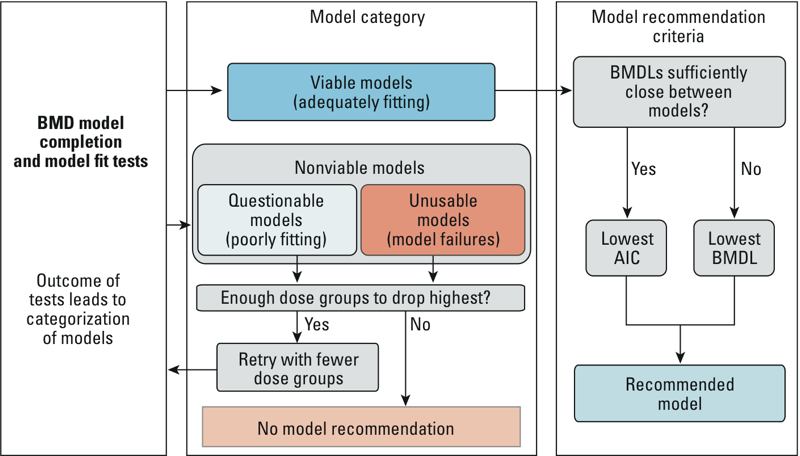
Model binning and recommendation. From Wignall et al. 2014.¶
If one and only one model is in the viable model bin, it is selected as the best-fitting model. If there are multiple models in the viable bin, then, consistent with EPA 2012, either the model with the lowest Akaike information criterion (AIC) or benchmark dose lower confidence limit (BMDL) is selected. If the range of BMDL values is sufficiently close (<3 fold different), the AIC value is used, otherwise, the BMDL value is used.
It is possible that some models may collapse into other models. For example, if a Power model doesn’t use the power-term after parameter optimization, then it may be equivalent to a Linear model. Or, a 3rd-order Polynomial may only use its first two polynomials, and therefore would be equivalent to a 2nd-order Polynomial. In these two examples, equivalent models will have identical AIC and BMDL values. In such cases, the recommendation logic will pick the model with the fewest number of parameters available for curve-fitting a priori to parameter optimization.
Therefore, in the examples above, the Linear and Polynomial 2 model will be selected as opposed to the Power or Polynomial 3 models, respectively.