Dichotomous Data with Bayesian Model Averaging¶
Bayesian model averaging is currently available for dichotomous datasets in pybmds. Here, we describe how to run a dichotomous analysis with Bayesian model averaging and how to plot your results. Also, we will demonstrate how you can override the default priors for parameter estimation.
Single model fit¶
You can run one model with the default prior distributions for the parameters, rather than running all of the models and finding the model average.
To run the Logistic model with the default prior distributions, see below. Note the model outputs show the prior distributions for a ~ Normal(0, 2), b ~ Lognormal(0, 2), and their constraints:
import pybmds
from pybmds.models import dichotomous
# create a dichotomous dataset
dataset = pybmds.DichotomousDataset(
doses=[0, 25, 75, 125, 200],
ns=[20, 20, 20, 20, 20],
incidences=[0, 1, 7, 15, 19],
)
model = dichotomous.Logistic(
dataset=dataset,
settings={"priors": pybmds.PriorClass.bayesian}
)
result = model.execute()
print(model.text())
Logistic Model
══════════════════════════════
Version: pybmds 24.1 (bmdscore 24.1)
Input Summary:
╒══════════════════════════════╤════════════════╕
│ BMR │ 10% Extra Risk │
│ Confidence Level (one sided) │ 0.95 │
│ Modeling approach │ bayesian │
│ Samples │ 100 │
│ Burn-in │ 20 │
╘══════════════════════════════╧════════════════╛
Parameter Settings:
╒═════════════╤════════════════╤═══════════╤═════════╤═══════╤═══════╕
│ Parameter │ Distribution │ Initial │ Stdev │ Min │ Max │
╞═════════════╪════════════════╪═══════════╪═════════╪═══════╪═══════╡
│ a │ Normal │ 0 │ 2 │ -20 │ 20 │
│ b │ Lognormal │ 0 │ 2 │ 0 │ 40 │
╘═════════════╧════════════════╧═══════════╧═════════╧═══════╧═══════╛
Modeling Summary:
╒════════════════╤════════════╕
│ BMD │ 40.0459 │
│ BMDL │ 29.5605 │
│ BMDU │ 52.896 │
│ AIC │ 84.2304 │
│ Log-Likelihood │ -40.1152 │
│ P-Value │ 0.678322 │
│ Overall d.f. │ 3.08389 │
│ Chi² │ 1.58231 │
╘════════════════╧════════════╛
Model Parameters:
╒════════════╤════════════╤════════════╤═════════════╕
│ Variable │ Estimate │ On Bound │ Std Error │
╞════════════╪════════════╪════════════╪═════════════╡
│ a │ -3.12092 │ no │ 0.586645 │
│ b │ 0.0321918 │ no │ 0.00594455 │
╘════════════╧════════════╧════════════╧═════════════╛
Goodness of Fit:
╒════════╤════════╤════════════╤════════════╤════════════╤═══════════════════╕
│ Dose │ Size │ Observed │ Expected │ Est Prob │ Scaled Residual │
╞════════╪════════╪════════════╪════════════╪════════════╪═══════════════════╡
│ 0 │ 20 │ 0 │ 0.84505 │ 0.0422525 │ -0.939325 │
│ 25 │ 20 │ 1 │ 1.79592 │ 0.0897962 │ -0.622527 │
│ 75 │ 20 │ 7 │ 6.60729 │ 0.330364 │ 0.186699 │
│ 125 │ 20 │ 15 │ 14.2315 │ 0.711576 │ 0.379305 │
│ 200 │ 20 │ 19 │ 19.3004 │ 0.965022 │ -0.365663 │
╘════════╧════════╧════════════╧════════════╧════════════╧═══════════════════╛
Analysis of Deviance:
╒═══════════════╤══════════════════╤════════════╤════════════╤═════════════╤═════════════╕
│ Model │ Log-Likelihood │ # Params │ Deviance │ Test d.f. │ P-Value │
╞═══════════════╪══════════════════╪════════════╪════════════╪═════════════╪═════════════╡
│ Full model │ -32.1362 │ 5 │ - │ - │ - │
│ Fitted model │ -40.1152 │ 2 │ 15.9579 │ 3 │ 0.00115676 │
│ Reduced model │ -68.0292 │ 1 │ 71.7859 │ 4 │ 9.54792e-15 │
╘═══════════════╧══════════════════╧════════════╧════════════╧═════════════╧═════════════╛
Change input settings¶
The default samples and burn-in are 100 and 20, respectively. The maximum number of samples is 1000.
You can change the burn-ins and samples:
model = dichotomous.Logistic(
dataset=dataset,
settings={
"priors": pybmds.PriorClass.bayesian,
"samples": 1000,
"burnin": 500
}
)
The maximum number of samples allowed is 1000.
Change parameter settings¶
Running a single Bayesian model with base configuration:
model = dichotomous.Logistic(
dataset=dataset, settings={"priors": pybmds.PriorClass.bayesian}
)
print(model.settings.tbl())
print(model.priors_tbl())
╒══════════════════════════════╤════════════════╕
│ BMR │ 10% Extra Risk │
│ Confidence Level (one sided) │ 0.95 │
│ Modeling approach │ bayesian │
│ Degree │ 0 │
│ Samples │ 100 │
│ Burn-in │ 20 │
╘══════════════════════════════╧════════════════╛
╒═════════════╤════════════════╤═══════════╤═════════╤═══════╤═══════╕
│ Parameter │ Distribution │ Initial │ Stdev │ Min │ Max │
╞═════════════╪════════════════╪═══════════╪═════════╪═══════╪═══════╡
│ a │ Normal │ 0 │ 2 │ -20 │ 20 │
│ b │ Lognormal │ 0 │ 2 │ 0 │ 40 │
╘═════════════╧════════════════╧═══════════╧═════════╧═══════╧═══════╛
Configuring the model settings or priors:
model = dichotomous.Logistic(
dataset=dataset,
settings={
"priors": pybmds.PriorClass.bayesian,
"samples": 1000,
"burnin": 500
}
)
model.settings.priors.update('a', stdev=1, min_value=-15, max_value=15)
model.settings.priors.update('b', stdev=3)
print(model.settings.tbl())
print(model.priors_tbl())
╒══════════════════════════════╤════════════════╕
│ BMR │ 10% Extra Risk │
│ Confidence Level (one sided) │ 0.95 │
│ Modeling approach │ bayesian │
│ Degree │ 0 │
│ Samples │ 1000 │
│ Burn-in │ 500 │
╘══════════════════════════════╧════════════════╛
╒═════════════╤════════════════╤═══════════╤═════════╤═══════╤═══════╕
│ Parameter │ Distribution │ Initial │ Stdev │ Min │ Max │
╞═════════════╪════════════════╪═══════════╪═════════╪═══════╪═══════╡
│ a │ Normal │ 0 │ 1 │ -15 │ 15 │
│ b │ Lognormal │ 0 │ 3 │ 0 │ 40 │
╘═════════════╧════════════════╧═══════════╧═════════╧═══════╧═══════╛
You can also change the parameter prior types from the default listed in the BMDS User Guide. Parameters can be given a Normal, Log-Normal, or Uniform distribution. These can be changed by:
model = dichotomous.Weibull(
dataset=dataset,
settings={
"priors": pybmds.PriorClass.bayesian,
"samples": 1000,
"burnin": 500
}
)
model.settings.priors.update(
'g', type=pybmds.PriorDistribution.Uniform, min_value=0, max_value=1
)
print(model.priors_tbl())
╒═════════════╤════════════════╤═══════════╤═════════╤═══════╤═══════╕
│ Parameter │ Distribution │ Initial │ Stdev │ Min │ Max │
╞═════════════╪════════════════╪═══════════╪═════════╪═══════╪═══════╡
│ g │ Uniform │ 0 │ 2 │ 0 │ 1 │
│ a │ Lognormal │ 0.424264 │ 0.5 │ 0 │ 40 │
│ b │ Lognormal │ 0 │ 1.5 │ 0 │ 10000 │
╘═════════════╧════════════════╧═══════════╧═════════╧═══════╧═══════╛
Or:
model.settings.priors.update(
'g',
type=pybmds.PriorDistribution.Lognormal,
min_value=0,
max_value=1,
initial_value=0,
stdev=1.5,
)
print(model.priors_tbl())
╒═════════════╤════════════════╤═══════════╤═════════╤═══════╤═══════╕
│ Parameter │ Distribution │ Initial │ Stdev │ Min │ Max │
╞═════════════╪════════════════╪═══════════╪═════════╪═══════╪═══════╡
│ g │ Lognormal │ 0 │ 1.5 │ 0 │ 1 │
│ a │ Lognormal │ 0.424264 │ 0.5 │ 0 │ 40 │
│ b │ Lognormal │ 0 │ 1.5 │ 0 │ 10000 │
╘═════════════╧════════════════╧═══════════╧═════════╧═══════╧═══════╛
Multiple model fit (sessions)¶
To run Bayesian model averaging:
import pybmds
from pybmds.models import dichotomous
# create a dichotomous dataset
dataset = pybmds.DichotomousDataset(
doses=[0, 25, 75, 125, 200],
ns=[20, 20, 20, 20, 20],
incidences=[0, 1, 7, 15, 19],
)
session = pybmds.Session(dataset=dataset)
session.add_default_bayesian_models()
session.execute()
res = session.model_average.results
print(f"BMD = {res.bmd:.2f} [{res.bmdl:.2f}, {res.bmdu:.2f}]")
session.plot(colorize=False)
BMD = 36.65 [17.83, 54.15]
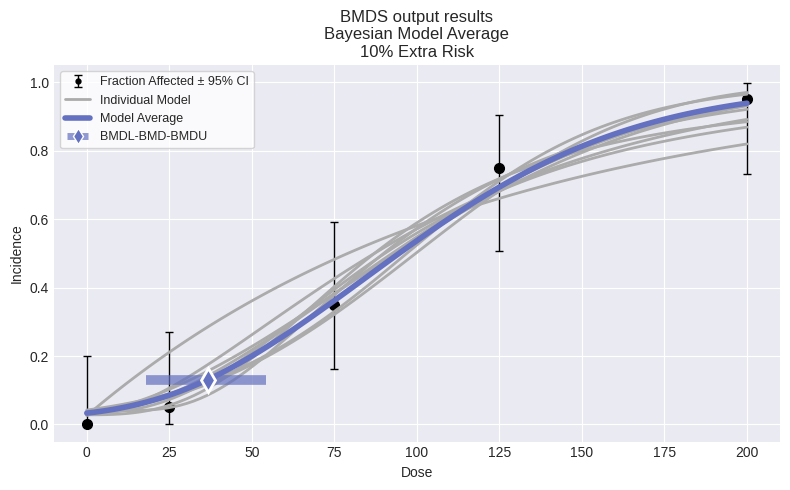
Change session settings¶
For a dichotomous Bayesian model average session, the default settings use a BMR of 10% Extra Risk and a 95% confidence interval. To change these settings:
session = pybmds.Session(dataset=dataset)
session.add_default_bayesian_models(
settings = {
"bmr": 0.05,
"bmr_type": pybmds.DichotomousRiskType.AddedRisk,
"alpha": 0.1
}
)
This would run the dichotomous models for a BMR of 5% Added Risk at a 90% confidence interval.
Run subset of models¶
Instead of running all available dichotomous models, you can select a subset of models.
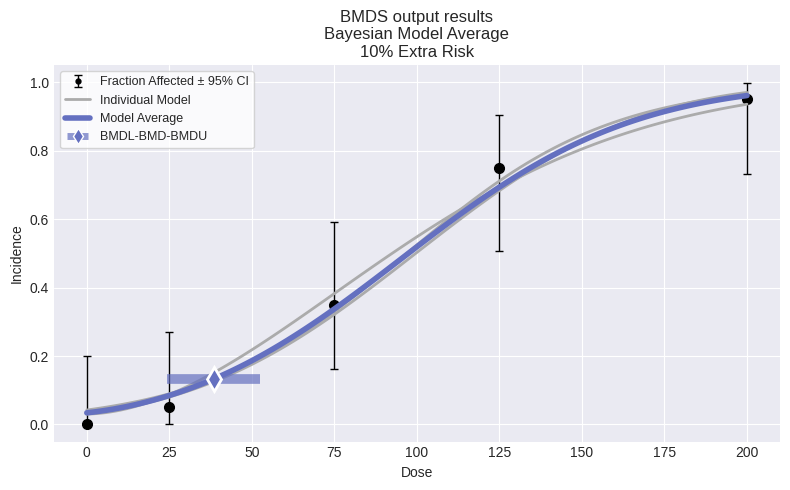
For example, to model average on the Logistic, Probit, and Weibull models:
session = pybmds.Session(dataset=dataset)
session.add_model(pybmds.Models.Weibull, {"priors": pybmds.PriorClass.bayesian})
session.add_model(pybmds.Models.Logistic, {"priors": pybmds.PriorClass.bayesian})
session.add_model(pybmds.Models.Probit, {"priors": pybmds.PriorClass.bayesian})
session.add_model_averaging()
session.execute()
res = session.model_average.results
print(f"BMD = {res.bmd:.2f} [{res.bmdl:.2f}, {res.bmdu:.2f}]")
session.plot(colorize=False)
BMD = 38.54 [24.43, 52.42]
