pybmds Quickstart¶
The pybmds package is designed for those familiar with basic scripting in languages like R or Python. In Python there are many different environments (jupyter notebooks, ipython, RStudio, Sypder, etc) commonly used for scripting; the example below will work in any of them.
The following example is recommended for people already familiar with scripting.
To create a dataset and fit a suite of dose-response models to the dataset:
import pybmds
# create a dataset
dataset = pybmds.DichotomousDataset(
doses=[0, 10, 50, 150, 400],
ns=[25, 25, 24, 24, 24],
incidences=[0, 3, 7, 11, 15],
)
# create a BMD session
session = pybmds.Session(dataset=dataset)
# add all default models
session.add_default_models()
# execute the session
session.execute()
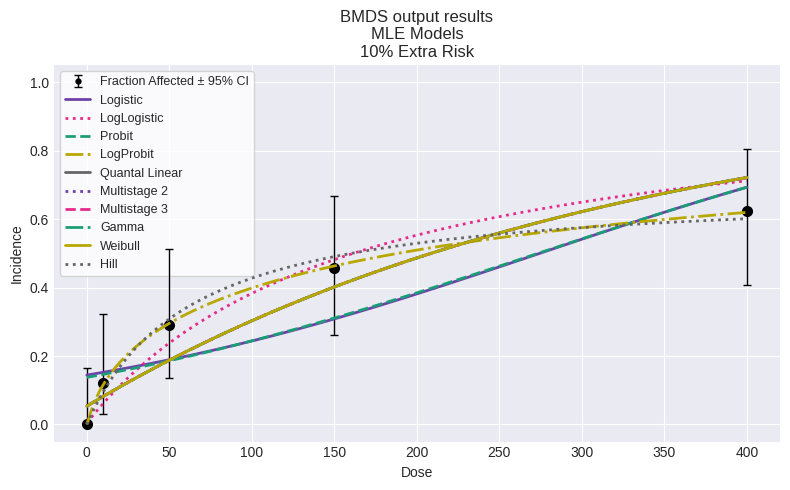
# show a summary figure
session.plot(colorize=True)

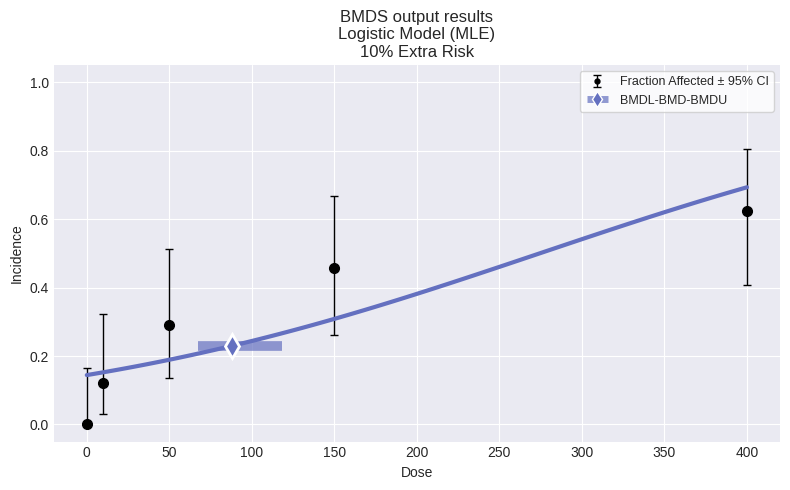
Show the first model output from the current session (i.e. Logistic):
first_model = session.models[0]
first_model.plot()

Detailed outputs are available with the results attribute on each model, or you can view a text summary of the model fit:
print(first_model.text())
Logistic Model
══════════════════════════════
Version: pybmds 25.2 (bmdscore 25.2)
Input Summary:
╒══════════════════════════════╤══════════════════════════╕
│ BMR │ 10% Extra Risk │
│ Confidence Level (one sided) │ 0.95 │
│ Modeling approach │ frequentist_unrestricted │
╘══════════════════════════════╧══════════════════════════╛
Parameter Settings:
╒═════════════╤═══════════╤═══════╤═══════╕
│ Parameter │ Initial │ Min │ Max │
╞═════════════╪═══════════╪═══════╪═══════╡
│ a │ 0 │ -18 │ 18 │
│ b │ 0 │ 0 │ 100 │
╘═════════════╧═══════════╧═══════╧═══════╛
Modeling Summary:
╒════════════════╤═════════════╕
│ BMD │ 88.0158 │
│ BMDL │ 67.4179 │
│ BMDU │ 117.983 │
│ AIC │ 128.521 │
│ Log-Likelihood │ -62.2605 │
│ P-Value │ 0.0278225 │
│ Overall d.f. │ 3 │
│ Chi² │ 9.11325 │
╘════════════════╧═════════════╛
Model Parameters:
╒════════════╤═════════════╤════════════╤═════════════╕
│ Variable │ Estimate │ On Bound │ Std Error │
╞════════════╪═════════════╪════════════╪═════════════╡
│ a │ -1.77998 │ no │ 0.308654 │
│ b │ 0.00648704 │ no │ 0.00143054 │
╘════════════╧═════════════╧════════════╧═════════════╛
Goodness of Fit:
╒════════╤════════╤════════════╤════════════╤════════════╤═══════════════════╕
│ Dose │ Size │ Observed │ Expected │ Est Prob │ Scaled Residual │
╞════════╪════════╪════════════╪════════════╪════════════╪═══════════════════╡
│ 0 │ 25 │ 0 │ 3.60765 │ 0.144306 │ -2.0533 │
│ 10 │ 25 │ 3 │ 3.81257 │ 0.152503 │ -0.452045 │
│ 50 │ 24 │ 7 │ 4.5393 │ 0.189138 │ 1.2826 │
│ 150 │ 24 │ 11 │ 7.40513 │ 0.308547 │ 1.58868 │
│ 400 │ 24 │ 15 │ 16.6353 │ 0.69314 │ -0.723809 │
╘════════╧════════╧════════════╧════════════╧════════════╧═══════════════════╛
Analysis of Deviance:
╒═══════════════╤══════════════════╤════════════╤════════════╤═════════════╤═════════════╕
│ Model │ Log-Likelihood │ # Params │ Deviance │ Test d.f. │ P-Value │
╞═══════════════╪══════════════════╪════════════╪════════════╪═════════════╪═════════════╡
│ Full model │ -56.09 │ 5 │ - │ - │ - │
│ Fitted model │ -62.2605 │ 2 │ 12.3409 │ 3 │ 0.00630208 │
│ Reduced model │ -74.01 │ 1 │ 35.84 │ 4 │ 3.12157e-07 │
╘═══════════════╧══════════════════╧════════════╧════════════╧═════════════╧═════════════╛
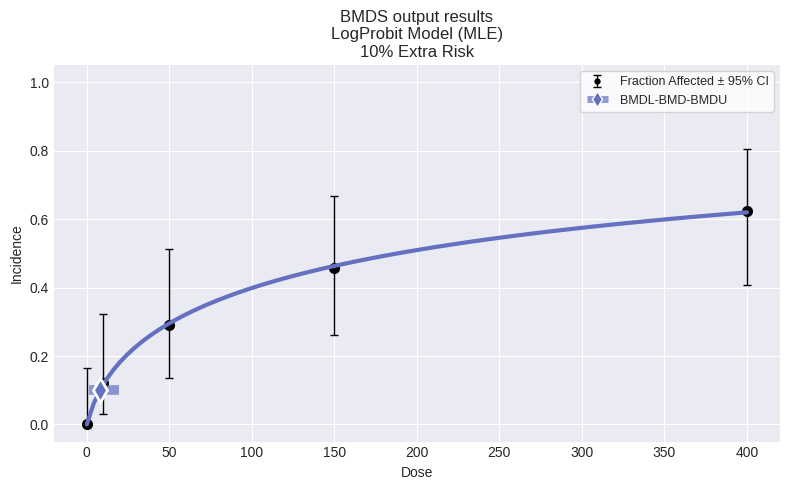
Recommend a best-fitting model from the collection of models used to fit the dataset:
session.recommend()
And show the recommended model:
print(session.recommended_model.text())
session.recommended_model.plot()
LogProbit Model
══════════════════════════════
Version: pybmds 25.2 (bmdscore 25.2)
Input Summary:
╒══════════════════════════════╤══════════════════════════╕
│ BMR │ 10% Extra Risk │
│ Confidence Level (one sided) │ 0.95 │
│ Modeling approach │ frequentist_unrestricted │
╘══════════════════════════════╧══════════════════════════╛
Parameter Settings:
╒═════════════╤═══════════╤══════════╤═══════╕
│ Parameter │ Initial │ Min │ Max │
╞═════════════╪═══════════╪══════════╪═══════╡
│ g │ 0 │ -18 │ 18 │
│ a │ 0 │ -18 │ 18 │
│ b │ 0.0001 │ 0.0001 │ 18 │
╘═════════════╧═══════════╧══════════╧═══════╛
Modeling Summary:
╒════════════════╤══════════════╕
│ BMD │ 7.96379 │
│ BMDL │ 1.16574 │
│ BMDU │ 19.7044 │
│ AIC │ 116.189 │
│ Log-Likelihood │ -56.0944 │
│ P-Value │ 0.999785 │
│ Overall d.f. │ 3 │
│ Chi² │ 0.00869929 │
╘════════════════╧══════════════╛
Model Parameters:
╒════════════╤════════════╤════════════╤══════════════╕
│ Variable │ Estimate │ On Bound │ Std Error │
╞════════════╪════════════╪════════════╪══════════════╡
│ g │ 1.523e-08 │ yes │ Not Reported │
│ a │ -2.122 │ no │ 0.504104 │
│ b │ 0.405055 │ no │ 0.107298 │
╘════════════╧════════════╧════════════╧══════════════╛
Standard errors estimates are not generated for parameters estimated on corresponding bounds,
although sampling error is present for all parameters, as a rule. Standard error estimates may not
be reliable as a basis for confidence intervals or tests when one or more parameters are on bounds.
Goodness of Fit:
╒════════╤════════╤════════════╤══════════════╤════════════╤═══════════════════╕
│ Dose │ Size │ Observed │ Expected │ Est Prob │ Scaled Residual │
╞════════╪════════╪════════════╪══════════════╪════════════╪═══════════════════╡
│ 0 │ 25 │ 0 │ 3.80749e-07 │ 1.523e-08 │ -0.000617049 │
│ 10 │ 25 │ 3 │ 2.92888 │ 0.117155 │ 0.0442273 │
│ 50 │ 24 │ 7 │ 7.09176 │ 0.29549 │ -0.0410505 │
│ 150 │ 24 │ 11 │ 11.1164 │ 0.463183 │ -0.0476461 │
│ 400 │ 24 │ 15 │ 14.8744 │ 0.619768 │ 0.0527974 │
╘════════╧════════╧════════════╧══════════════╧════════════╧═══════════════════╛
Analysis of Deviance:
╒═══════════════╤══════════════════╤════════════╤════════════╤═════════════╤═════════════╕
│ Model │ Log-Likelihood │ # Params │ Deviance │ Test d.f. │ P-Value │
╞═══════════════╪══════════════════╪════════════╪════════════╪═════════════╪═════════════╡
│ Full model │ -56.09 │ 5 │ - │ - │ - │
│ Fitted model │ -56.0944 │ 2 │ 0.00869649 │ 3 │ 0.999785 │
│ Reduced model │ -74.01 │ 1 │ 35.84 │ 4 │ 3.12157e-07 │
╘═══════════════╧══════════════════╧════════════╧════════════╧═════════════╧═════════════╛